Some 3D Problems Separable in Cartesian Coordinates

We begin our study of Quantum Mechanics in 3 dimensions with a few simple cases of problems that can be separated in Cartesian coordinates. This is possible when the Hamiltonian can be written

$$\bgroup\color{black}H=H_x+H_y+H_z.\egroup$$

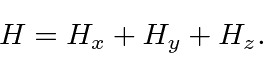
One nice example of separation of variable in Cartesian coordinates is the 3D harmonic oscillator

$$\bgroup\color{black}V(r)={1\over 2}m\omega^2r^2\egroup$$

which has energies which depend on three quantum numbers.

$$\bgroup\color{black}E_{n_xn_yn_z}=\left(n_x+n_y+n_z+{3\over 2}\right)\hbar\omega\egroup$$

It really behaves like 3 independent one dimensional harmonic oscillators.

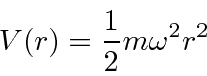
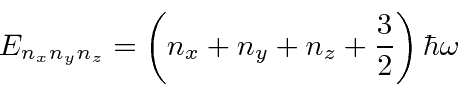
Another problem that separates is the particle in a 3D box. Again, energies depend on three quantum numbers

$$\bgroup\color{black}E_{n_xn_yn_z}={\pi^2\hbar^2\over 2mL^2}\left(n_x^2+n_y^2+n_z^2\right)\egroup$$

for a cubic box of side $L$. We investigate the effect of the Pauli exclusion principle by filling our 3D box with identical fermions which must all be in different states. We can use this to model White Dwarfs or Neutron Stars.

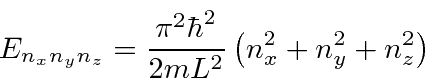
In classical physics, it takes three coordinates to give the location of a particle in 3D. In quantum mechanics, we are finding that it takes three quantum numbers to label and energy eigenstate (not including spin).