Next: Solutions to the Radial Up: Course Summary Previous: Some 3D Problems Separable Contents
For the common
problem of central potentials
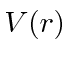 ,
we use the obvious rotational symmetry to find that the angular momentum,
,
we use the obvious rotational symmetry to find that the angular momentum,
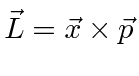 , operators commute with
, operators commute with
![]() ,
,
![\begin{displaymath}\bgroup\color{black}[H,L_z]=[H,L_x]=[H,L_y]=0\egroup\end{displaymath}](img234.png)
![\begin{displaymath}\bgroup\color{black}[L_x,L_y]\neq 0\egroup\end{displaymath}](img235.png)
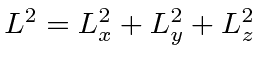 which does commute with each component of
which does commute with each component of
![\begin{displaymath}\bgroup\color{black}[L^2,L_z]=0\egroup\end{displaymath}](img237.png)
Some computation reveals that we can write
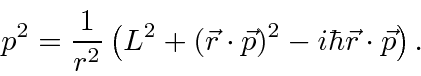
![\begin{displaymath}\bgroup\color{black}{-\hbar^2\over 2\mu}\left[{1\over r^2}\le...
... r^2}\right] u_E(\vec{r})+V(r)u_E(\vec{r})=Eu_E(\vec{r})\egroup\end{displaymath}](img242.png)
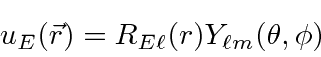
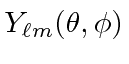 will be eigenfunctions of
will be eigenfunctions of
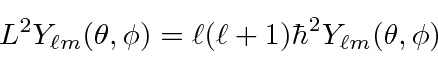
![\begin{displaymath}\bgroup\color{black}{-\hbar^2\over 2\mu}\left[{1\over r^2}\le...
... r^2}\right] R_{E\ell}(r)+V(r)R_{E\ell}(r)=ER_{E\ell}(r)\egroup\end{displaymath}](img246.png)
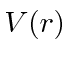 which we want to solve.
which we want to solve.
We solve the angular part of the problem in general
using angular momentum operators.
We find that angular momentum is quantized.
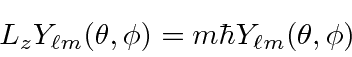
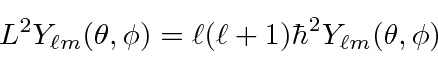
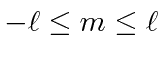 .
The operators that raise and lower the
.
The operators that raise and lower the 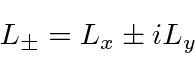
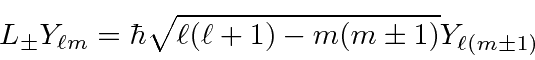
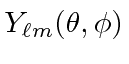 using the differential form of the angular momentum operators.
using the differential form of the angular momentum operators.
Jim Branson 2013-04-22