Next: Hydrogen Up: Course Summary Previous: Angular Momentum Contents
Solutions to the
radial equation
in a constant potential are important since they are the solutions for large
![]() in potentials of limitted range.
They are therefore used in scattering problems as the incoming and outgoing states.
The solutions are the
spherical Bessel and spherical Neumann functions.
in potentials of limitted range.
They are therefore used in scattering problems as the incoming and outgoing states.
The solutions are the
spherical Bessel and spherical Neumann functions.
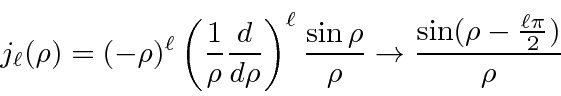
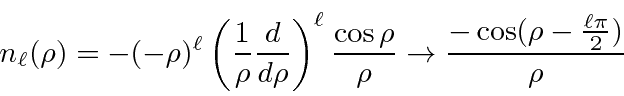
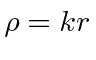 .
The linear combination of these which falls off properly at large
.
The linear combination of these which falls off properly at large
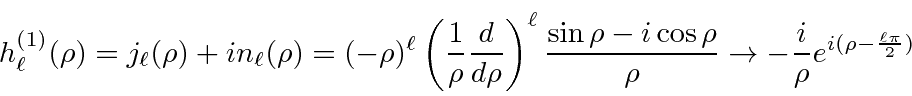
We use these solutions to do a partial wave analysis of scattering, solve for bound states of a spherical potential well, solve for bound states of an infinite spherical well (a spherical ``box''), and solve for scattering from a spherical potential well.