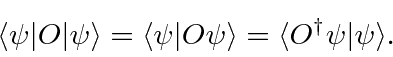For any given physical problem, the
Schrödinger equation solutions which separate
(between time and space),
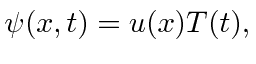 are an extremely important set.
If we assume the equation separates, we get the two equations (in one dimension for simplicity)
are an extremely important set.
If we assume the equation separates, we get the two equations (in one dimension for simplicity)
The second equation is called the time independent Schrödinger equation.
For bound states, there are only solutions to that equation for some quantized set of energies
For states which are not bound, a continuous range of energies is allowed.
The time independent Schrödinger equation is an example of an
eigenvalue equation.
If we operate on
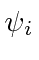 with
with
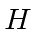 , we get back the same function
, we get back the same function
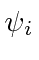 times some constant.
In this case
times some constant.
In this case
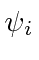 would be called and Eigenfunction, and
would be called and Eigenfunction, and
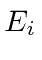 would be called an Eigenvalue.
There are usually an infinite number of solutions, indicated by the index
would be called an Eigenvalue.
There are usually an infinite number of solutions, indicated by the index
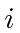 here.
here.
Operators for physical variables must have real eigenvalues.
They are called
Hermitian operators.
We can show that the eigenfunctions of Hermitian operators are orthogonal (and can be normalized).
(In the case of eigenfunctions with the same eigenvalue, called degenerate eigenfunctions,
we can must choose linear combinations which are orthogonal to each other.)
We will assume that the
eigenfunctions also form a complete set so that any wavefunction can be expanded in them,
where the
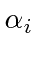 are coefficients which can be easily computed (due to orthonormality) by
are coefficients which can be easily computed (due to orthonormality) by
So now we have another way to represent a state (in addition to position space and momentum space).
We can represent a state by giving the coefficients in sum above.
(Note that
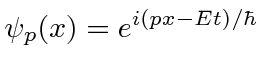 is just an eigenfunction of the momentum operator and
is just an eigenfunction of the momentum operator and
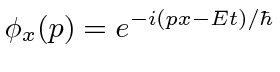 is just an eigenfunction of the position operator (in p-space)
so they also represent and expansion of the state in terms of eigenfunctions.)
is just an eigenfunction of the position operator (in p-space)
so they also represent and expansion of the state in terms of eigenfunctions.)
Since the
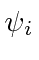 form an orthonormal, complete set, they can be thought of as the unit vectors
of a
vector space.
The arbitrary wavefunction
form an orthonormal, complete set, they can be thought of as the unit vectors
of a
vector space.
The arbitrary wavefunction
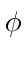 would then be a vector in that space and could be
represented by its coefficients.
would then be a vector in that space and could be
represented by its coefficients.
The bra-ket
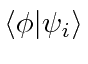 can be thought of as a dot product between the
arbitrary vector
can be thought of as a dot product between the
arbitrary vector
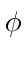 and one of the unit vectors.
We can use the expansion in terms of energy eigenstates to compute many things.
In particular, since the time development of the energy eigenstates is very simple,
and one of the unit vectors.
We can use the expansion in terms of energy eigenstates to compute many things.
In particular, since the time development of the energy eigenstates is very simple,
we can use these eigenstates to follow the time development of an arbitrary state
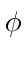
simply by computing the coefficients
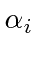 at
at
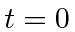 .
.
We can define the
Hermitian conjugate
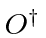 of the operator
of the operator
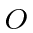 by
by
Hermitian operators
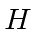 have the property that
have the property that
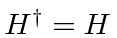 .
.
Jim Branson
2013-04-22
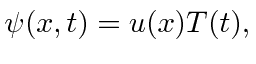 are an extremely important set.
If we assume the equation separates, we get the two equations (in one dimension for simplicity)
are an extremely important set.
If we assume the equation separates, we get the two equations (in one dimension for simplicity)
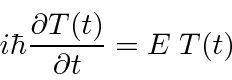
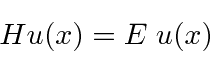
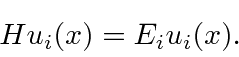
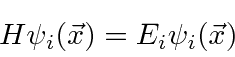
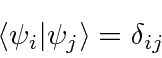
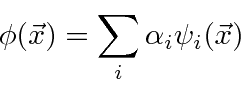
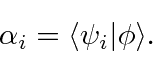
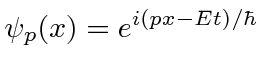 is just an eigenfunction of the momentum operator and
is just an eigenfunction of the momentum operator and
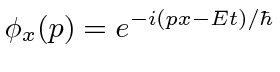 is just an eigenfunction of the position operator (in p-space)
so they also represent and expansion of the state in terms of eigenfunctions.)
is just an eigenfunction of the position operator (in p-space)
so they also represent and expansion of the state in terms of eigenfunctions.)
![]() form an orthonormal, complete set, they can be thought of as the unit vectors
of a
vector space.
The arbitrary wavefunction
form an orthonormal, complete set, they can be thought of as the unit vectors
of a
vector space.
The arbitrary wavefunction
![]() would then be a vector in that space and could be
represented by its coefficients.
would then be a vector in that space and could be
represented by its coefficients.
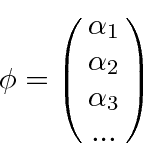
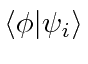 can be thought of as a dot product between the
arbitrary vector
can be thought of as a dot product between the
arbitrary vector
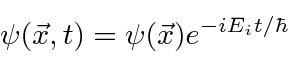
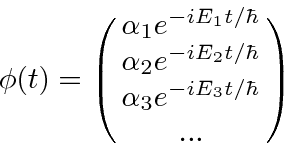
![]() of the operator
of the operator
![]() by
by