The Schrödinger Equation

Wave functions must satisfy the Schrödinger Equation which is actually a wave equation.

$$\bgroup\color{black}{-\hbar^2 \over 2m}\nabla^2\psi(\vec{x},t... ...vec{x},t)=i\hbar{\partial\psi(\vec{x},t)\over\partial t}\egroup$$

We will use it to solve many problems in this course. In terms of operators, this can be written as

$$\bgroup\color{black}H\psi(\vec{x},t)=E\psi(\vec{x},t)\egroup$$

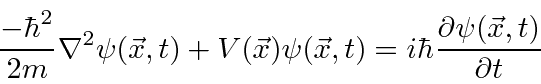
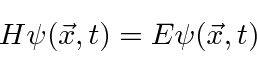
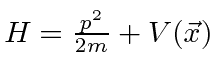where (dropping the $(op)$ label) $H={p^2\over 2m}+V(\vec{x})$ is the Hamiltonian operator. So the Schrödinger Equation is, in some sense, simply the statement (in operators) that the kinetic energy plus the potential energy equals the total energy.