Next: The Harmonic Oscillator in Up: Course Summary Previous: A Particle in a Contents
We now study the physics of several
simple potentials in one dimension.
First a series of piecewise
constant potentials
for which the Schrödinger equation is
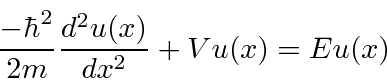
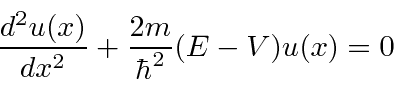
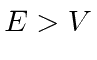 , can be written as either
, can be written as either
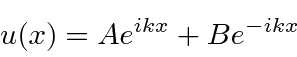
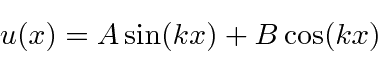
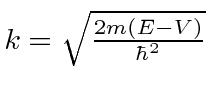 .
We will also need solutions for the classically forbidden regions where the total
energy is less than the potential energy,
.
We will also need solutions for the classically forbidden regions where the total
energy is less than the potential energy,
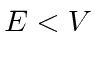 .
.

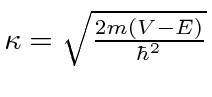 .
(Both
.
(Both
First, we calculate the probability the a particle of energy
![]() is reflected by a
potential step
of height
is reflected by a
potential step
of height
![]() :
:
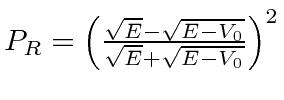 .
We also use this example to understand the probability current
.
We also use this example to understand the probability current
![\bgroup\color{black}$j={\hbar\over 2im}[u^*{du\over dx}-{du^*\over dx}u]$\egroup](img146.png) .
.
Second we investigate the
square potential well
square potential well
(
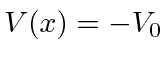 for
for
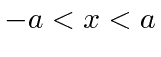 and
and
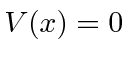 elsewhere),
for the case where the particle is not bound
elsewhere),
for the case where the particle is not bound
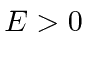 .
Assuming a beam of particles incident from the left,
we need to match solutions in the three regions at the boundaries at
.
Assuming a beam of particles incident from the left,
we need to match solutions in the three regions at the boundaries at
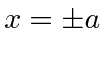 .
After some difficult arithmetic, the probabilities to be transmitted or reflected are computed.
It is found that the probability to be transmitted goes to 1 for some particular energies.
.
After some difficult arithmetic, the probabilities to be transmitted or reflected are computed.
It is found that the probability to be transmitted goes to 1 for some particular energies.
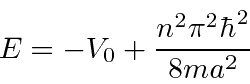
Third we study the
square potential barrier
(
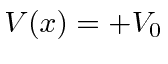 for
for
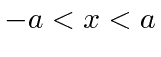 and
and
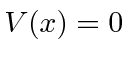 elsewhere),
for the case in which
elsewhere),
for the case in which
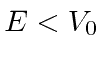 .
Classically the probability to be transmitted would be zero since the
particle is energetically excluded from being inside the barrier.
The Quantum calculation gives the probability to be transmitted through the barrier to be
.
Classically the probability to be transmitted would be zero since the
particle is energetically excluded from being inside the barrier.
The Quantum calculation gives the probability to be transmitted through the barrier to be
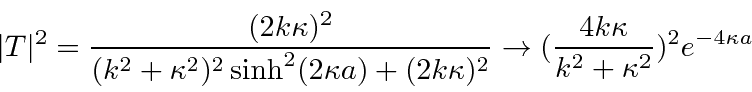
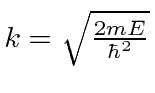 and
and
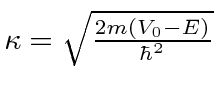 .
Study of this expression shows that the probability to be transmitted decreases as
the barrier get higher or wider.
Nevertheless, barrier penetration is an important quantum phenomenon.
.
Study of this expression shows that the probability to be transmitted decreases as
the barrier get higher or wider.
Nevertheless, barrier penetration is an important quantum phenomenon.
We also study the
square well for the bound state
case in which
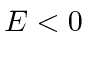 .
Here we need to solve a transcendental equation to determine the bound state energies.
The number of bound states increases with the depth and the width of the well but there is
always at least one bound state.
.
Here we need to solve a transcendental equation to determine the bound state energies.
The number of bound states increases with the depth and the width of the well but there is
always at least one bound state.
Jim Branson 2013-04-22