The Potential Well with $E>0$ *

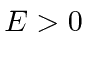With positive energy, this is again a scattering type problem, now with three regions of the potential, all with $E>V$.

$$\bgroup\color{black} V(x)=\left\{ \matrix{0 & x<-a \cr -V_0 & -a<x<a \cr 0& x>a\cr} \right. \egroup$$

Numbering the three regions from left to right,

$$\begin{eqnarray*} u_1(x)=e^{ikx}+Re^{-ikx} \\ u_2(x)=Ae^{ik'x}+Be^{-ik'x} \\ u_3(x)=Te^{ikx} \\ \end{eqnarray*}$$

Again we have assumed a beam of definite momentum incident from the left and no wave incident from the right.

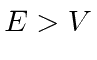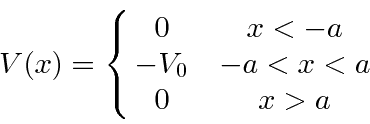
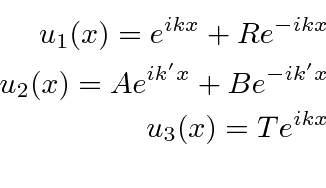
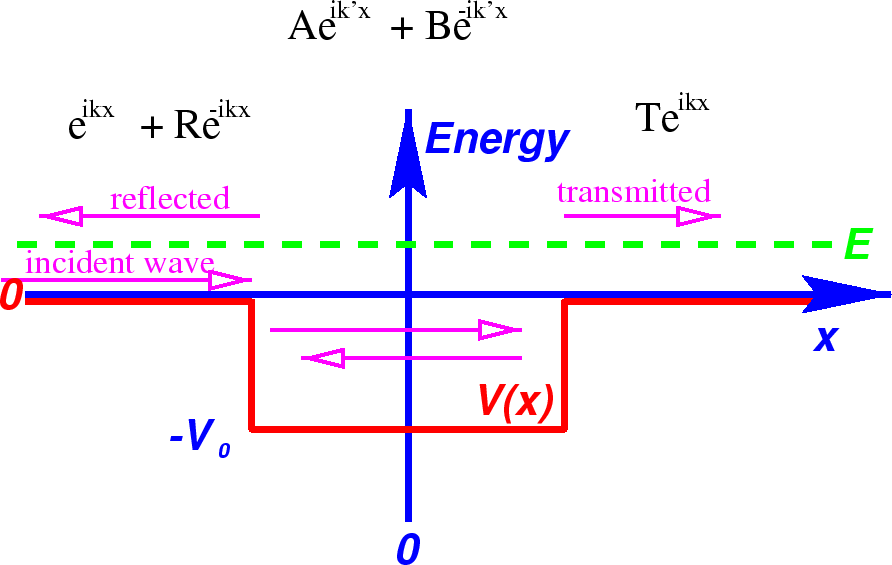
There are four unknown coefficients. We now match the wave function and its first derivative at the two boundaries yielding 4 equations.

Some hard work yields the reflection and transmission amplitudes

$$\begin{eqnarray*} R&=&ie^{-2ika}{(k'^2-k^2)\sin(2k'a)\over 2kk'\cos(2k'a)-i(k'^2... ...=&e^{-2ika}{2kk'\over 2kk'\cos(2k'a)-i(k'^2+k^2)\sin(2k'a)} .\\ \end{eqnarray*}$$

The squares of these give the reflection and transmission probability, since the potential is the same in the two regions.

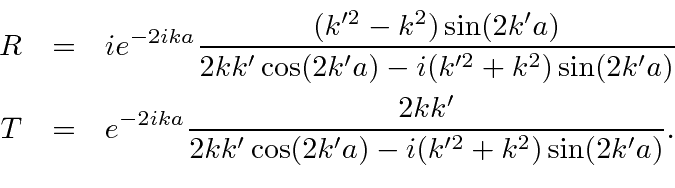
Again, classically, everything would be transmitted because the energy is larger than the potential. Quantum mechanically, there is a probability to be transmitted and a probability to be reflected. The reflection probability will go to zero for certain energies: $R\rightarrow 0$ if

$$\begin{eqnarray*} 2k'a=n\pi \\ k'=\sqrt{2m(E-V_0)\over\hbar^2} \\ E=-V_0+{n^2\pi^2\hbar^2\over 8ma^2} \\ \end{eqnarray*}$$

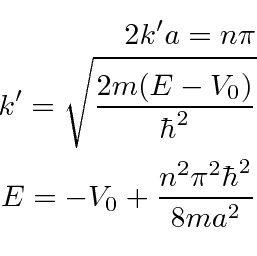
There are analogs of this in 3D. The scattering cross section often goes to zero for certain particular energies. For example, electrons scattering off atoms may have nearly zero cross section at some particular energy. Again this is a wave property.