Next: The Potential Well with Up: Piecewise Constant Potentials in Previous: The General Solution for Contents
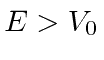 .
.
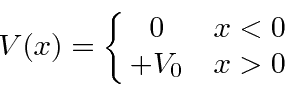
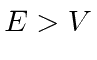 ,
so we will use the complex exponential solutions in both regions.
This is essentially a 1D scattering problem.
Assume there is a beam of particles with definite momentum
coming in from the left and assume there is no flux of particles coming from the right.
,
so we will use the complex exponential solutions in both regions.
This is essentially a 1D scattering problem.
Assume there is a beam of particles with definite momentum
coming in from the left and assume there is no flux of particles coming from the right.
For
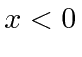 , the solution is
, the solution is
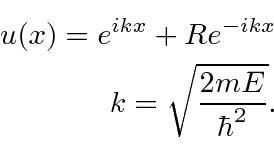
 the solution is
the solution is
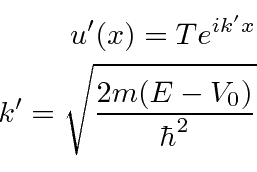
 .)
.)
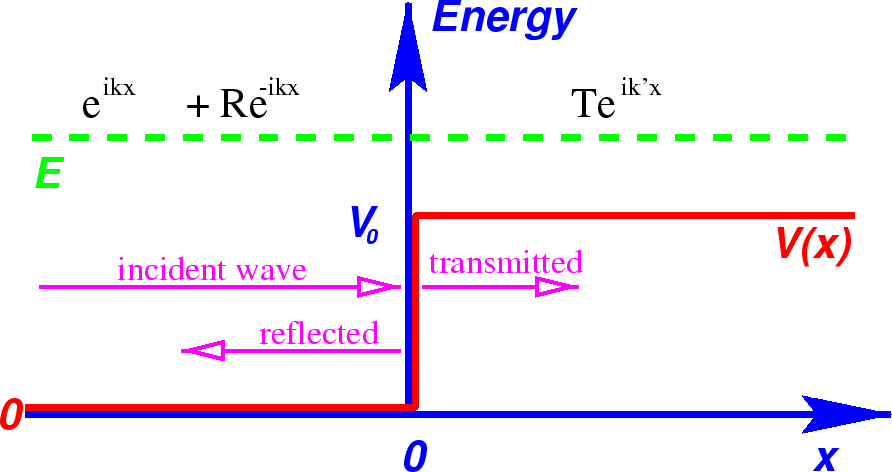
There are two unknown coefficients
![]() and
and
![]() which will be determined by matching boundary conditions.
We will not require normalization to one particle, since we have a beam with definite momentum,
which cannot be so normalized.
(A more physical problem to solve would use an incoming wave packet with a spread in momentum.)
which will be determined by matching boundary conditions.
We will not require normalization to one particle, since we have a beam with definite momentum,
which cannot be so normalized.
(A more physical problem to solve would use an incoming wave packet with a spread in momentum.)
Continuity of the wave function at
![]() implies
implies
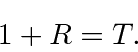
Continuity of the derivative of the wavefunction at
![]() gives
gives
![\begin{displaymath}\bgroup\color{black} [ike^{ikx}-ikRe^{-ikx}]_{x=0}=[ik'Te^{ik'x}]_{x=0} \egroup\end{displaymath}](img1232.png)
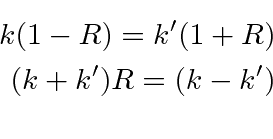
The coefficients are
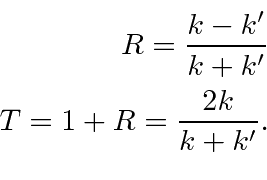
We now have the full solution, given our assumption of particles incident from the left.
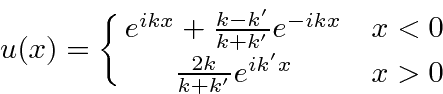
Classically, all of the particles would be transmitted, continuing on to infinity.
In Quantum Mechanics, some probability is reflected.
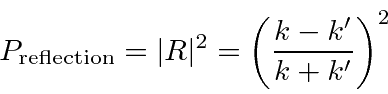
If we wish to compute the transmission probability, the easy way to do it is to say that its
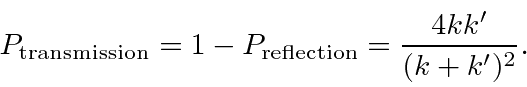
We'll get the same answers for the reflection and transmission coefficients using the probability flux to solve the problem.
The transmission probability goes to 1 one
![]() (since there is no step).
The transmission probability goes to 0 for
(since there is no step).
The transmission probability goes to 0 for
![]() (since the kinetic energy is zero).
(since the kinetic energy is zero).
Jim Branson 2013-04-22