Next: Dirac Particle at Rest Up: Dirac Equation Previous: The Non-Relativistic Equation Contents
We can show that a free particle solution can be written as a constant spinor times the usual free particle exponential. Start from the Dirac equation and attempt to develop an equation to show that each component has the free particle exponential. We will do this by making a second order differential equation, which turns out to be the Klein-Gordon equation.
 |
 |
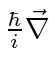 and the energy operator is still
and the energy operator is still
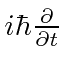 .
.
There is no coupling between the different components in this equation, but,
we will see that (unlike the equation differentiated again)
the Dirac equation will give us relations between the components of the constant spinor.
Again, the solution can be written as a constant spinor, which may depend on momentum
![]() , times the exponential.
, times the exponential.
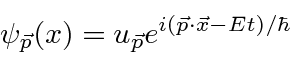
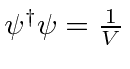 .
We haven't learned much about what each component represents yet.
We also have the plus or minus in the relation
.
We haven't learned much about what each component represents yet.
We also have the plus or minus in the relation
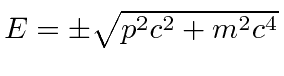 to deal with.
The solutions for a free particle at rest will tell us more about what the different components mean.
to deal with.
The solutions for a free particle at rest will tell us more about what the different components mean.