Next: Solution of Dirac Equation Up: The Non-relativistic Limit of Previous: The Large and Small Contents
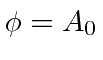 .
The energy we have been using in our non-relativistic formulation is
.
The energy we have been using in our non-relativistic formulation is
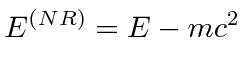 .
We will work with the equation for the large component
.
We will work with the equation for the large component 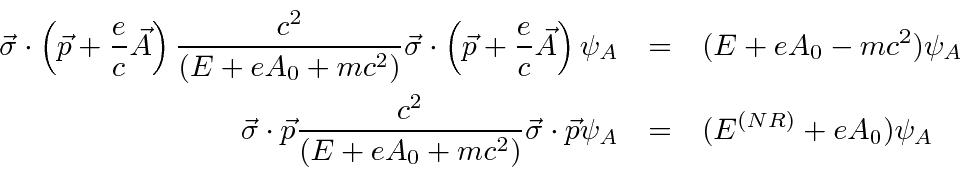
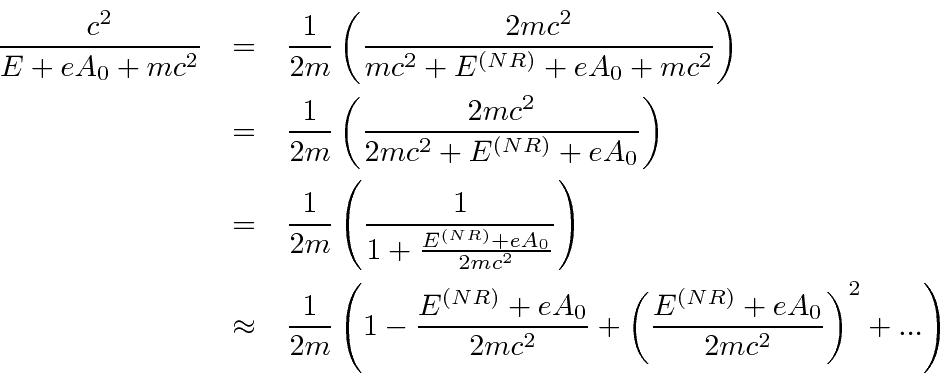
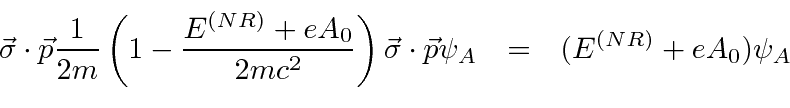
The normalization condition we derive from the Dirac equation is
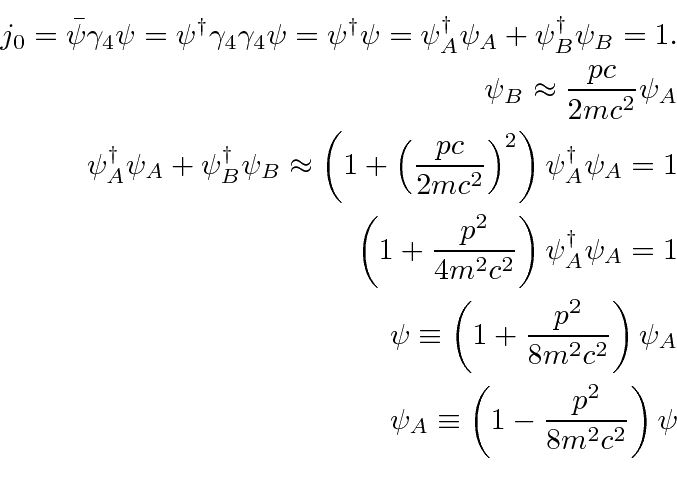
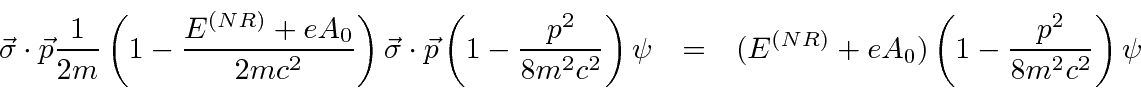
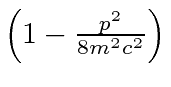 .
.
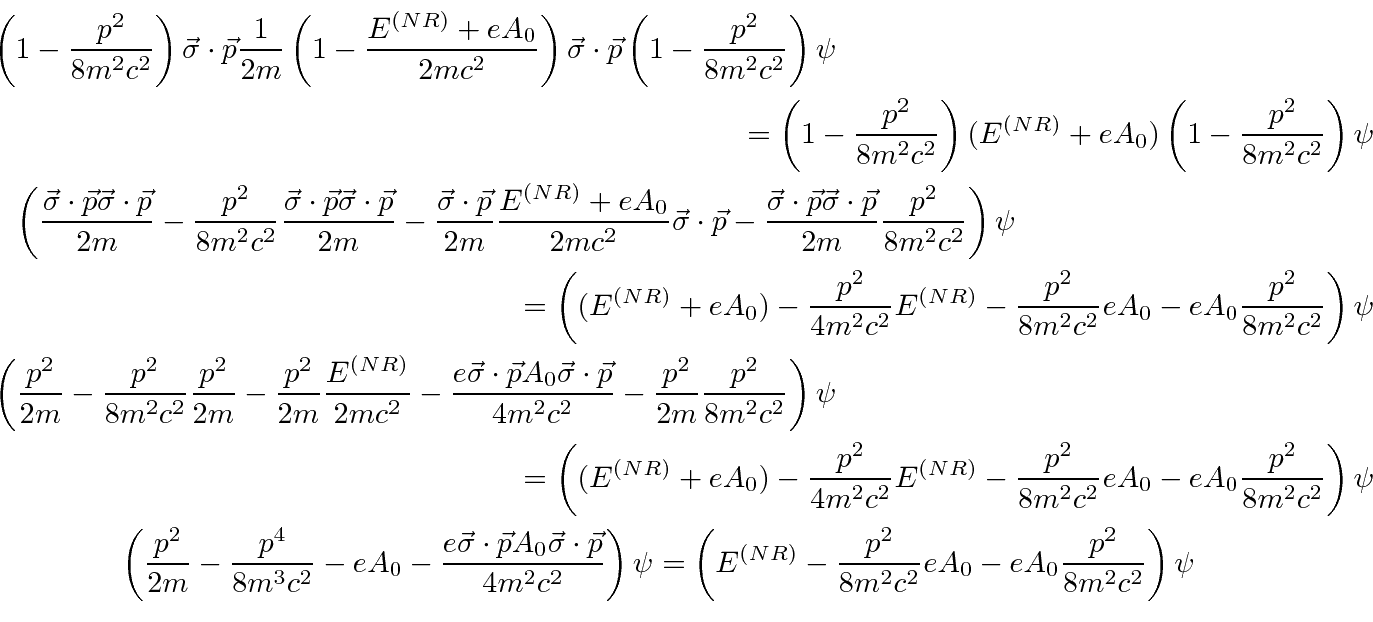
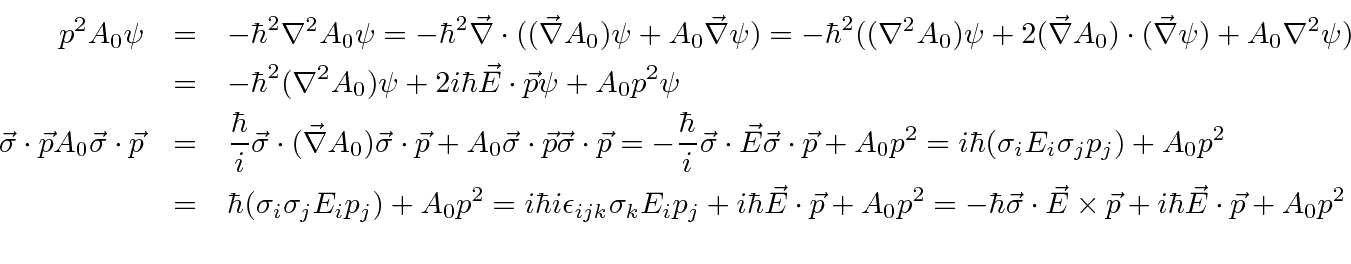
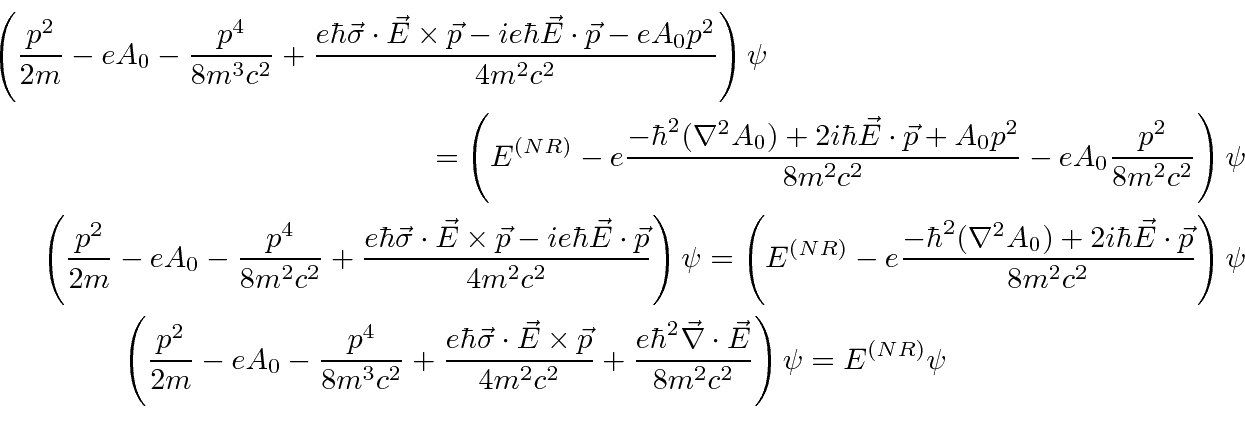
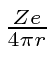 in our new units.
We identify
in our new units.
We identify
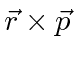 as the orbital angular momentum.
Note that
as the orbital angular momentum.
Note that
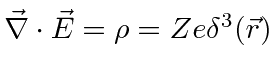 .
The equation can now be cast in a more familiar form.
.
The equation can now be cast in a more familiar form.
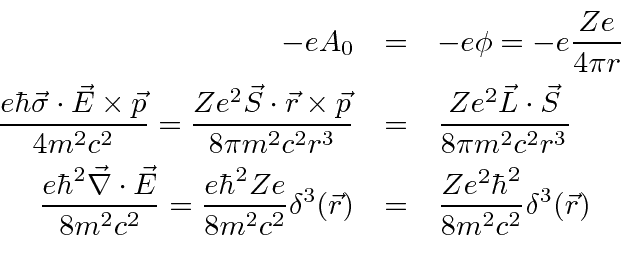
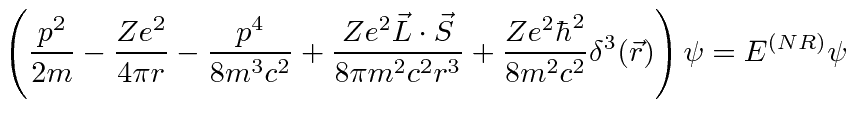 |
This ``Schrödinger equation'', derived from the Dirac equation, agrees well with the one we used to understand
the fine structure of Hydrogen.
The first two terms are the kinetic and potential energy terms for the unperturbed Hydrogen Hamiltonian.
Note that our units now put a
![]() in the denominator here.
(The
in the denominator here.
(The
![]() will be absorbed into the new formula for
will be absorbed into the new formula for
![]() .)
The third term is the relativistic correction to the kinetic energy.
The fourth term is the correct spin-orbit interaction, including the Thomas Precession effect that we did not
take the time to understand when we did the NR fine structure.
The fifth term is the so called Darwin term which we said would come from the Dirac equation;
and now it has.
.)
The third term is the relativistic correction to the kinetic energy.
The fourth term is the correct spin-orbit interaction, including the Thomas Precession effect that we did not
take the time to understand when we did the NR fine structure.
The fifth term is the so called Darwin term which we said would come from the Dirac equation;
and now it has.
This was an important test of the Dirac equation and it passed with flying colors. The Dirac equation naturally incorporates relativistic corrections, the interaction with electron spin, and gives an additional correction for s states that is found to be correct experimentally. When the Dirac equation is used to make a quantum field theory of electrons and photons, Quantum ElectroDynamics, we can calculate effects to very high order and compare the calculations with experiment, finding good agreement.
Jim Branson 2013-04-22