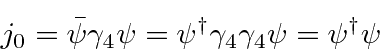Next: The Non-Relativistic Equation Up: The Non-relativistic Limit of Previous: The Two Component Dirac Contents
 .
Note that for
.
Note that for
 .
.
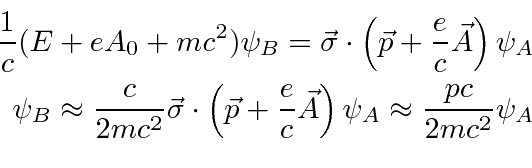
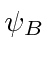 would be of order
would be of order
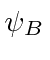 the small component.
When we include relativistic corrections for the fine structure of Hydrogen, we must consider the effect
the small component.
When we include relativistic corrections for the fine structure of Hydrogen, we must consider the effect
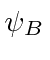 has on the normalization.
Remember that the conserved current indicates that the normalization condition for the four component Dirac spinor is.
has on the normalization.
Remember that the conserved current indicates that the normalization condition for the four component Dirac spinor is.