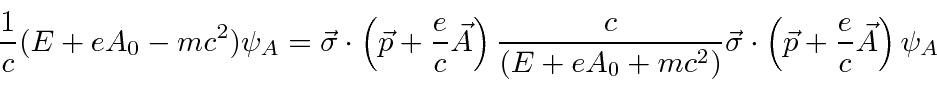First, we can write the two component equation that is equivalent to the Dirac equation.
Assume that the solution has the usual time dependence
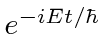 .
We start from the equation in
.
We start from the equation in
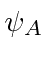 and
and
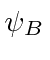 .
.
Turn on the EM field by making the usual substitution
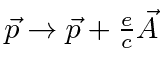 and adding the
scalar potential term.
and adding the
scalar potential term.
These two equations can be turned into one by eliminating
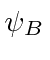 .
.
This is the two component equation which is equivalent to the Dirac equation for energy eigenstates.
The one difference from our understanding of the Dirac equation is in the normalization.
We shall see below that the normalization difference is small for non-relativistic electron states
but needs to be considered for atomic fine structure.
Jim Branson
2013-04-22
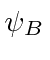 .
.
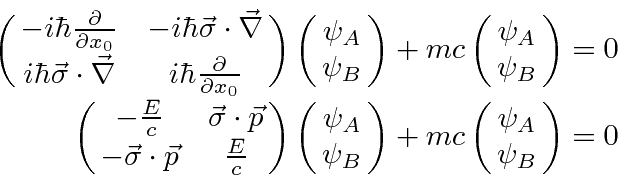
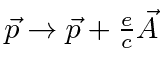 and adding the
scalar potential term.
and adding the
scalar potential term.
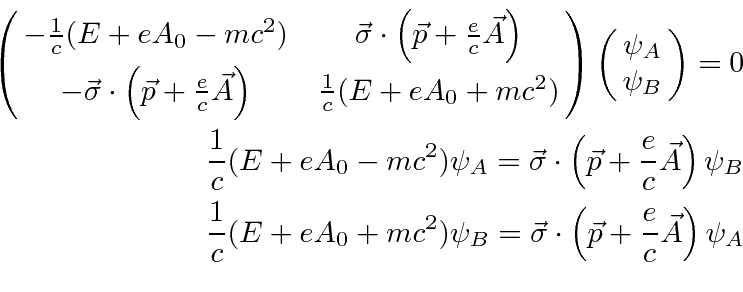
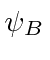 .
.