Next: The Two Component Dirac Up: Dirac Equation Previous: The Conserved Probability Current Contents
We know that our non-relativistic Quantum Mechanics only needed a two component spinor.
We can show that, in the non-relativistic limit, two components of the Dirac spinor are large
and two are quite small.
To do this, we go back to the equations written in terms of
![]() and
and
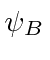 ,
just prior to the introduction of the
,
just prior to the introduction of the
![]() matrices.
We make the substitution to put the couplings to the electromagnetic field into the Hamiltonian.
matrices.
We make the substitution to put the couplings to the electromagnetic field into the Hamiltonian.