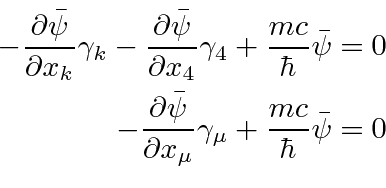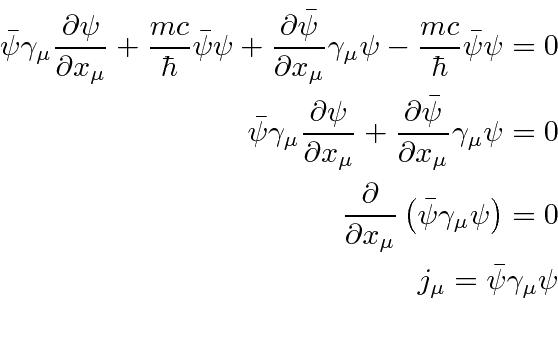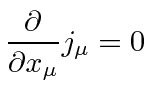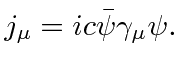We now return to the nagging problem of the probability density and current which prompted Dirac to find an
equation that is first order in the time derivative.
We
derived the equation showing conservation of probability
for 1D Schrödinger theory by
using the Schrödinger equation and its complex conjugate to get an equation of the form
We also extended it to three dimensions in the same way.
Our problem to find a similar probability and flux for Dirac theory is similar but a little more difficult.
Start with the Dirac equation.
Since the wave function is a 4 component spinor, we will use the Hermitian conjugate of the Dirac equation
instead of the complex conjugate.
The
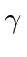 matrices are Hermitian.
matrices are Hermitian.
The complex conjugate does nothing to the spatial component of
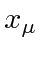 but does change the sign of the fourth component.
To turn this back into a 4-vector expression, we can change the sign back by multiplying the equation by
but does change the sign of the fourth component.
To turn this back into a 4-vector expression, we can change the sign back by multiplying the equation by
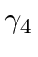 (from the right).
(from the right).
Defining
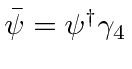 , the adjoint spinor, we can rewrite the Hermitian conjugate equation.
, the adjoint spinor, we can rewrite the Hermitian conjugate equation.
This is the adjoint equation.
We now multiply the Dirac equation by
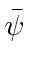 from the left and
multiply the adjoint equation by
from the left and
multiply the adjoint equation by
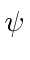 from the right, and subtract.
from the right, and subtract.
We have found a conserved current.
Some interpretation will be required as we learn more about the solutions to the Dirac equation and ultimately quantize it.
We may choose an overall constant to set the normalization.
The fourth component of the current should be
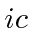 times the probability density so that the derivative with
respect to
times the probability density so that the derivative with
respect to
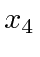 turns into
turns into
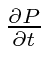 .
Therefore let us set the properly normalized conserved 4-vector to be
.
Therefore let us set the properly normalized conserved 4-vector to be
Jim Branson
2013-04-22
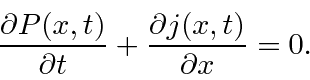
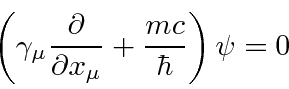
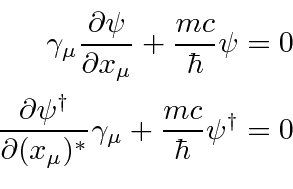
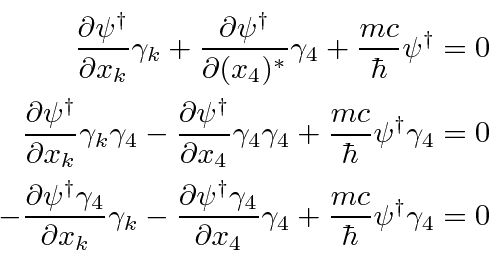
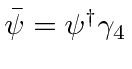 , the adjoint spinor, we can rewrite the Hermitian conjugate equation.
, the adjoint spinor, we can rewrite the Hermitian conjugate equation.