Next: Alternate Labeling of the Up: Solution of Dirac Equation Previous: Dirac Particle at Rest Contents
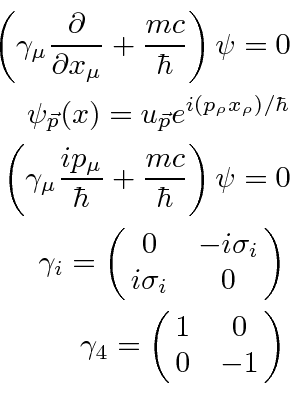
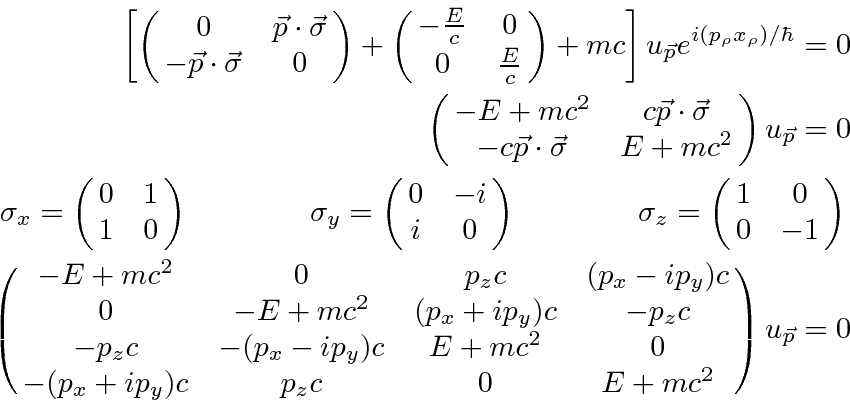
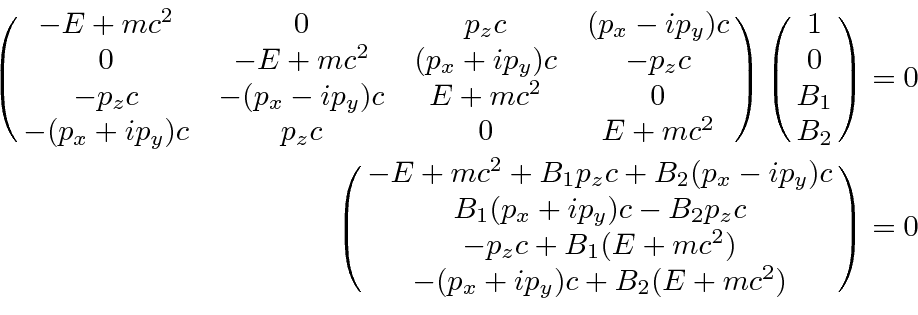
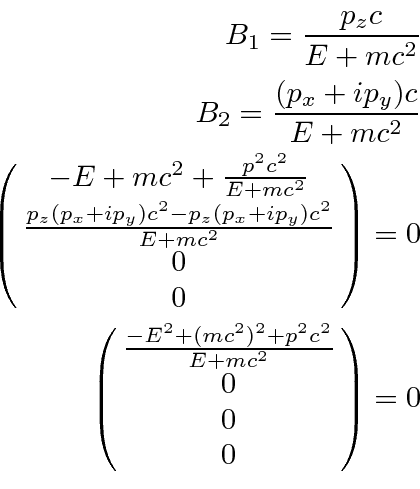
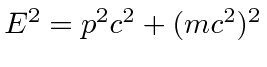 , not a surprising condition.
Adding a normalization factor, the solution is.
, not a surprising condition.
Adding a normalization factor, the solution is.
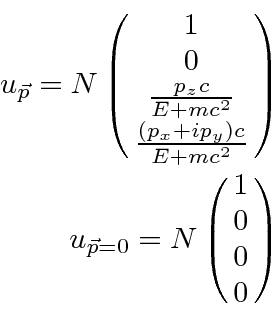
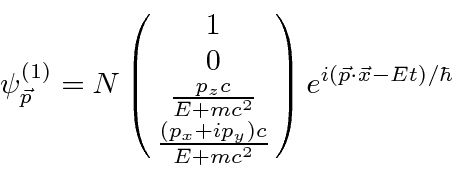
If we make the upper two components those of a spin down electron, we get the next solution following the same procedure.
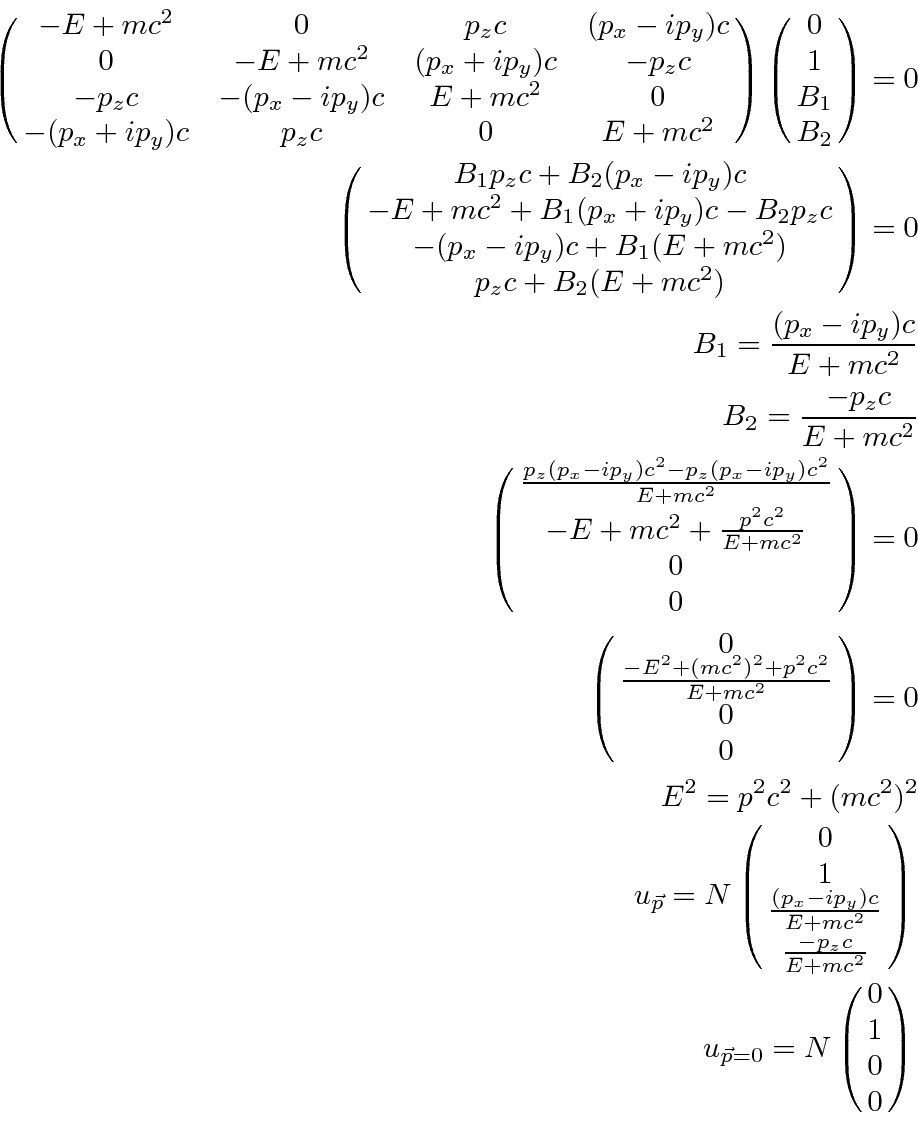
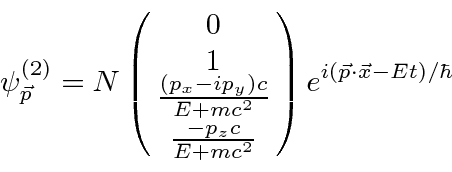
Now we take a look at the ``negative energy'' spin up solution in the same way.
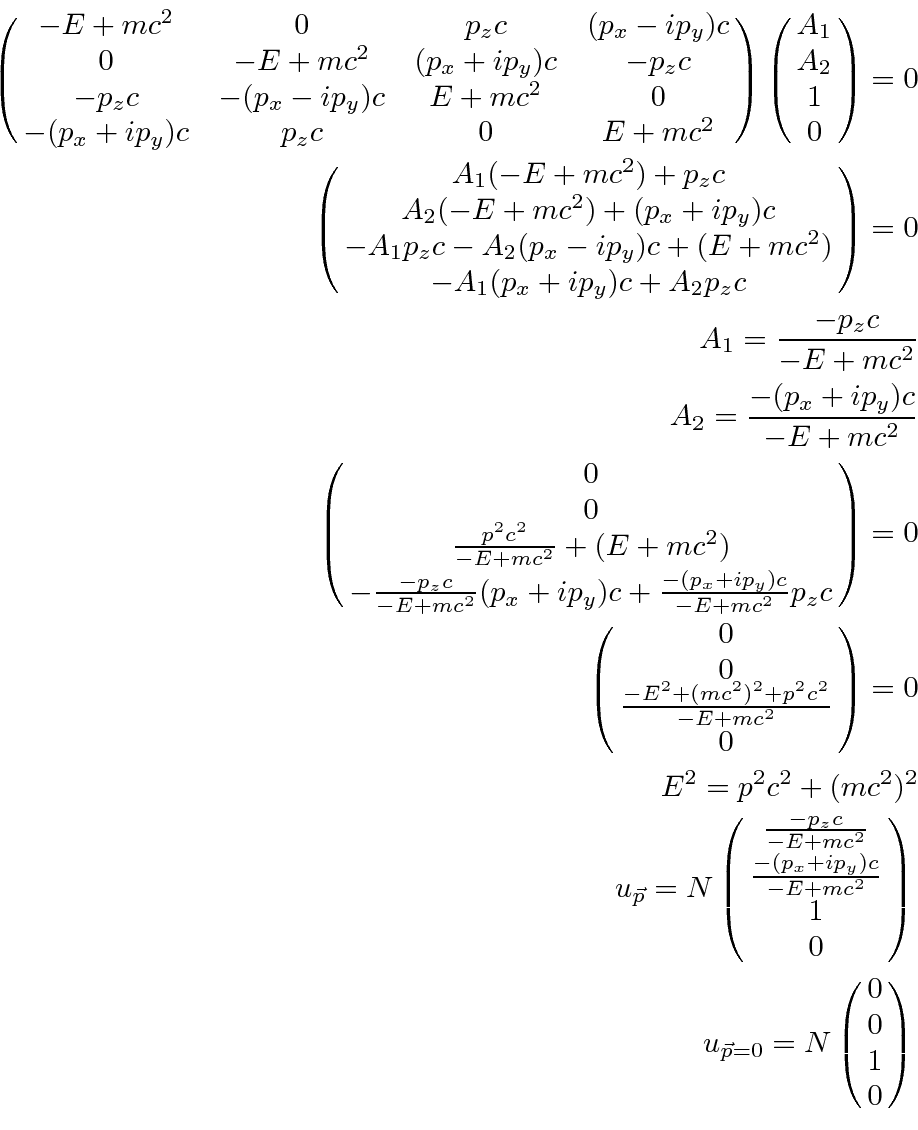
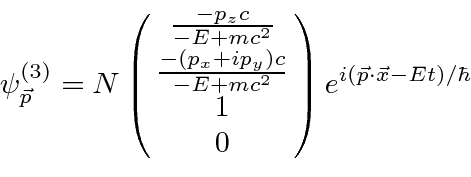
Finally, the ``negative energy'', spin down solution follows the same pattern.
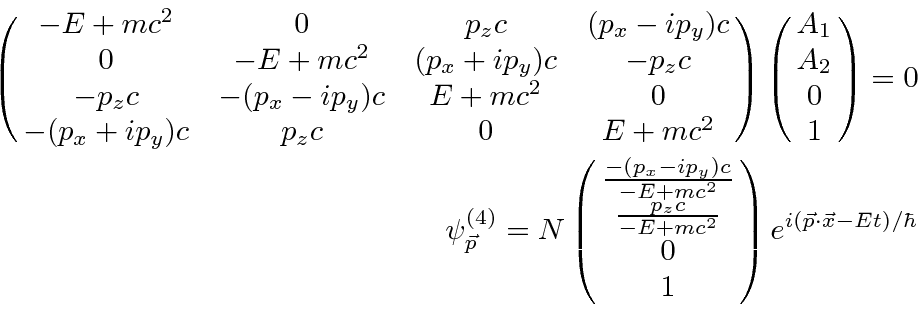
We will normalize the states so that there is one particle per unit volume.
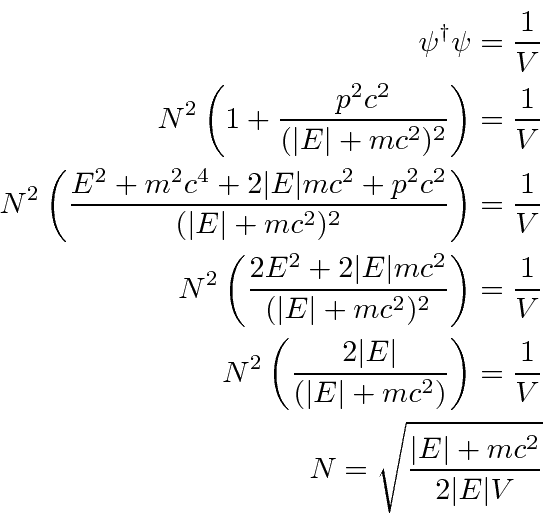
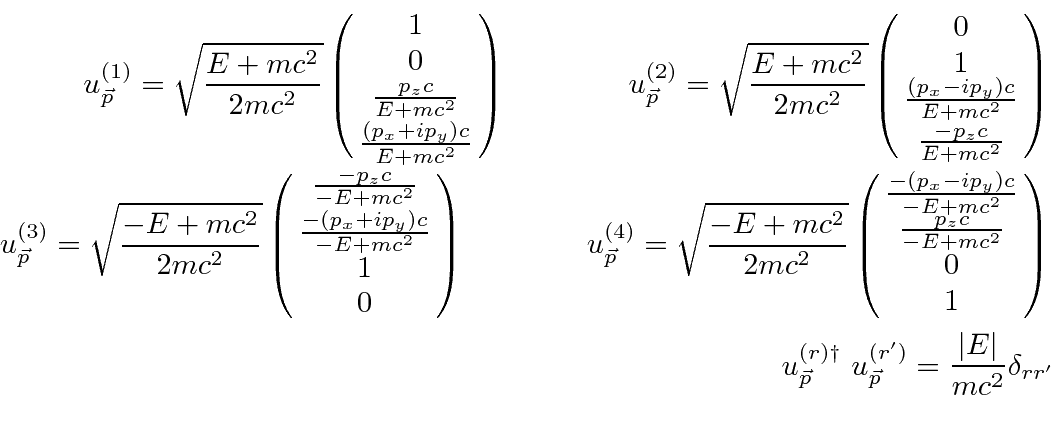
We have the four solutions with for a free particle with momentum ![]() .
For solutions 1 and 2,
.
For solutions 1 and 2,
![]() is a positive number.
For solutions 3 and 4,
is a positive number.
For solutions 3 and 4,
![]() is negative.
is negative.
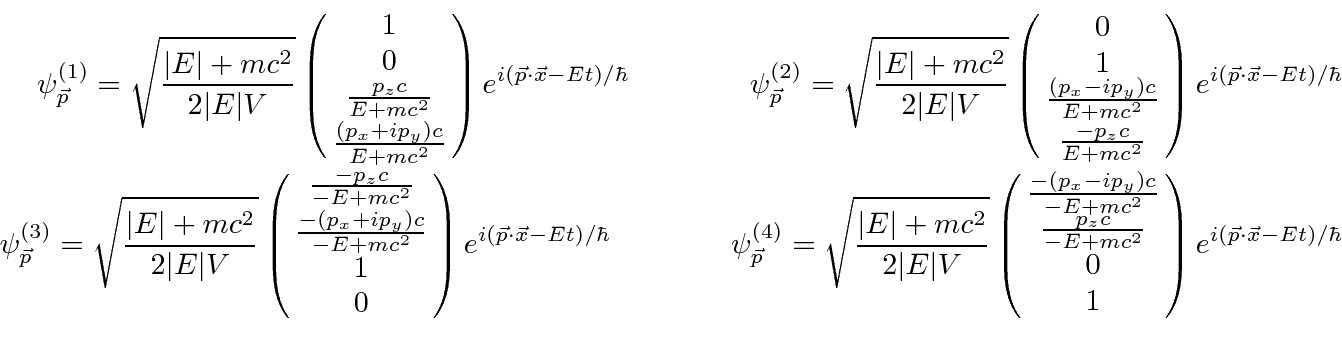
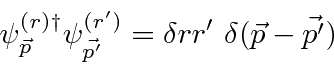
It is useful to write the plane wave states as a spinor
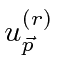 times an exponential.
Sakurai picks a normalization of the spinor so that
times an exponential.
Sakurai picks a normalization of the spinor so that
![]() transforms like the fourth component of a vector.
We will follow the same convention.
transforms like the fourth component of a vector.
We will follow the same convention.
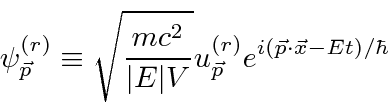
Are the free particle states still eigenstates of
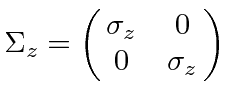 as were the states of a particle at rest?
In general, they are not.
To have an eigenvalue of +1, a spinor must have zero second and fourth components
and to have an eigenvalue of -1, the first and third components must be zero.
So boosting our Dirac particle to a frame in which it is moving, mixes up the spin states.
as were the states of a particle at rest?
In general, they are not.
To have an eigenvalue of +1, a spinor must have zero second and fourth components
and to have an eigenvalue of -1, the first and third components must be zero.
So boosting our Dirac particle to a frame in which it is moving, mixes up the spin states.
There is one case for which these are still spin eigenstates.
If the particle's momentum is in the z direction, then we have just the spinors we need to be eigenstates of
![]() .
That is, if we boost along the quantization axis, the spin eigenstates are preserved.
These are called helicity eigenstates.
Helicity is the spin component along the direction of the particle.
While it is possible to make definite momentum solutions which are eigenstates of helicity,
it is not possible to make definite momentum states which are eigenstates of spin along some other direction
(except in the trivial case of
.
That is, if we boost along the quantization axis, the spin eigenstates are preserved.
These are called helicity eigenstates.
Helicity is the spin component along the direction of the particle.
While it is possible to make definite momentum solutions which are eigenstates of helicity,
it is not possible to make definite momentum states which are eigenstates of spin along some other direction
(except in the trivial case of
 as we have shown).
as we have shown).
To further understand these solutions, we can compute the conserved probability current. First, compute it in general for a Dirac spinor
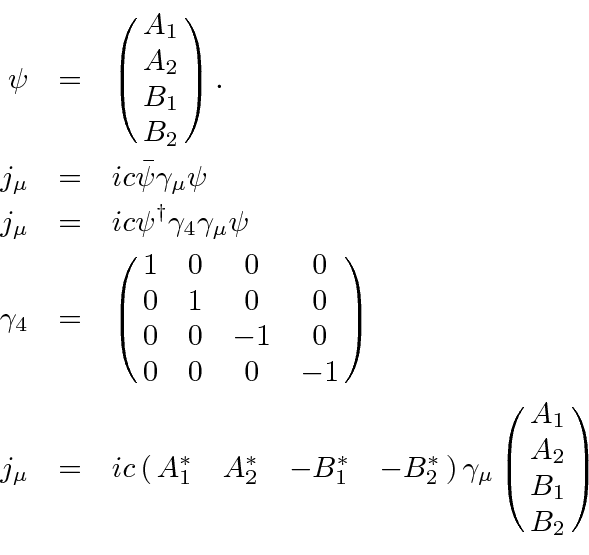
![\begin{eqnarray*}
\gamma_1&=&\pmatrix{0 & 0 & 0 & -i \cr 0 & 0 & -i & 0 \cr 0 & ...
...A_2^*B_2-A_2B_2^*\cr i[A_1^*A_1+A_2^*A_2+B_1^*B_1+B_2^*B_2]} \\
\end{eqnarray*}](img4265.png)
 ,
and a ``negative energy'' plane wave,
,
and a ``negative energy'' plane wave,
 .
.
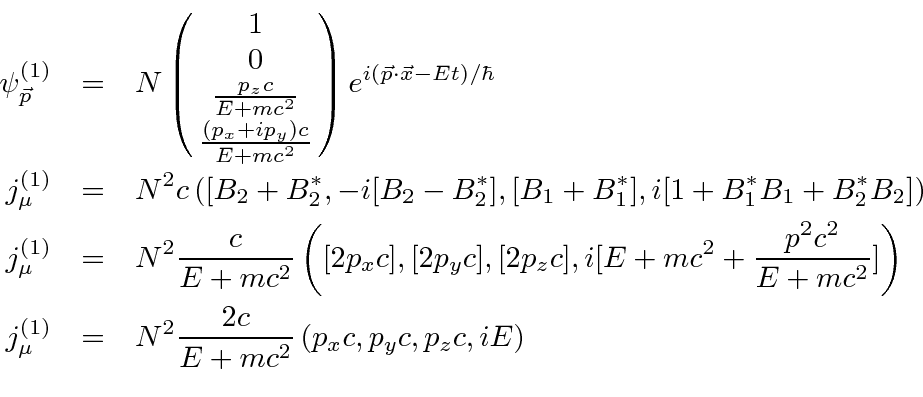
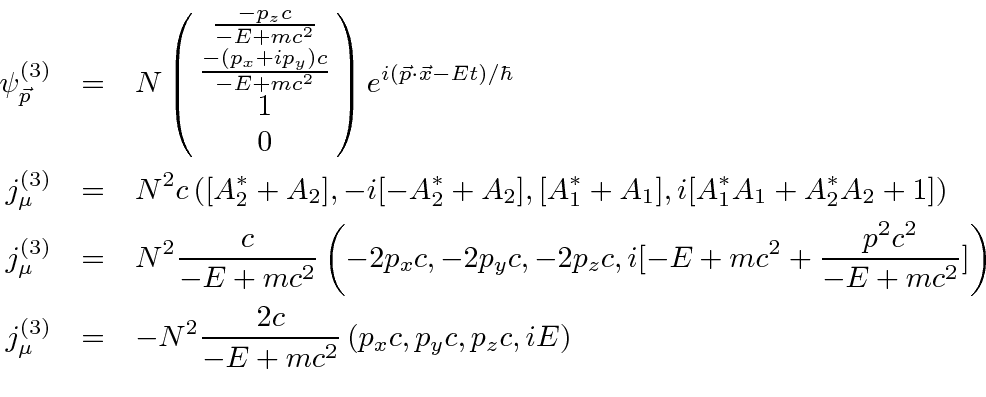
Jim Branson 2013-04-22