Start from the four plane wave solutions: 1 and 2 with positive energy and 3 and 4 with negative.
There are four solutions for each choice of momentum
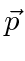 .
.
Concentrate on the exponential which determines the wave property.
For solutions 3 and 4, both the phase and group velocity are in the opposite direction to the momentum,
indicating we have a problem that was not seen in non-relativistic quantum mechanics.
Clearly, we want waves that propagate in the right direction.
Perhaps the momentum and energy operators we developed in NR quantum mechanics are not the whole story.
For solutions 3 and 4, pick the solution for
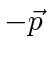 to classify with solutions 1 and 2 with momentum
to classify with solutions 1 and 2 with momentum
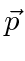 write everything in terms of the positive square root
write everything in terms of the positive square root
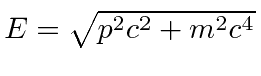 .
.
We have plane waves of the form
which is not very surprising.
In fact we picked the + sign somewhat randomly in the development of NR quantum mechanics.
For relativistic quantum mechanics, both solutions are needed.
We have no good reason to associate the
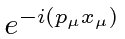 solution with negative energy.
Lets assume it also has positive energy but happens to have the - sign on the whole exponent.
solution with negative energy.
Lets assume it also has positive energy but happens to have the - sign on the whole exponent.
Consider the Dirac equation with the EM field term included.
(While we are dealing with free particle solutions, we can consider that nearly free particles will have a very similar
exponential term.)
The
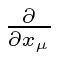 operating on the exponential produces
operating on the exponential produces
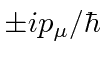 .
If we change the charge on the electron from
.
If we change the charge on the electron from
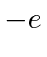 to
to
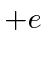 and change the sign of the exponent, the equation remains the same.
Thus, we can turn the negative exponent solution (going backward in time) into the conventional positive exponent
solution if we change the charge to
and change the sign of the exponent, the equation remains the same.
Thus, we can turn the negative exponent solution (going backward in time) into the conventional positive exponent
solution if we change the charge to
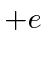 .
Recall that the momentum has already been inverted (and the spin also will be inverted).
.
Recall that the momentum has already been inverted (and the spin also will be inverted).
The negative exponent electron solutions can be recast as conventional exponent positron solutions.
Jim Branson
2013-04-22
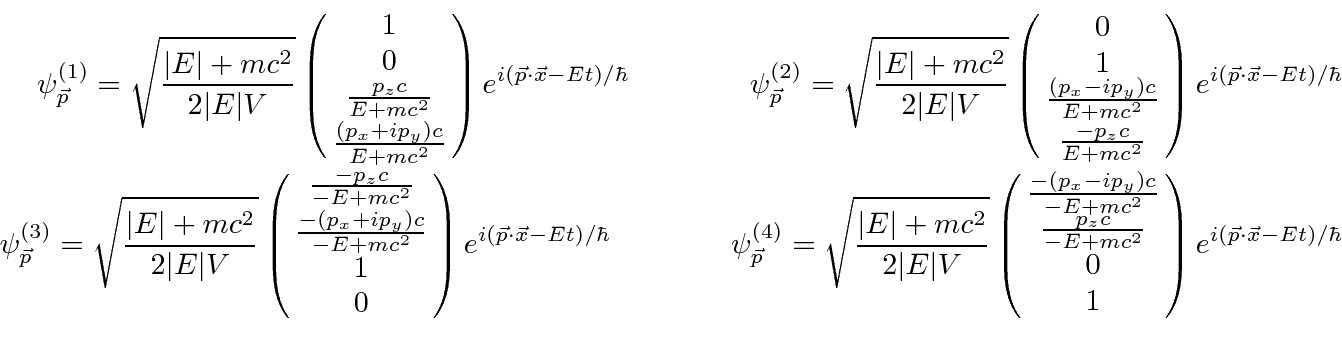
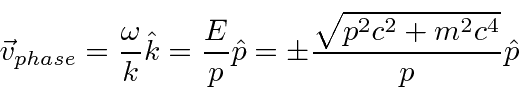
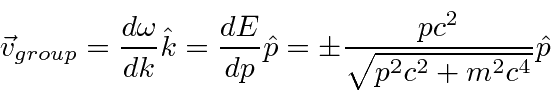
![]() to classify with solutions 1 and 2 with momentum
to classify with solutions 1 and 2 with momentum
![]() write everything in terms of the positive square root
write everything in terms of the positive square root
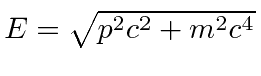 .
.
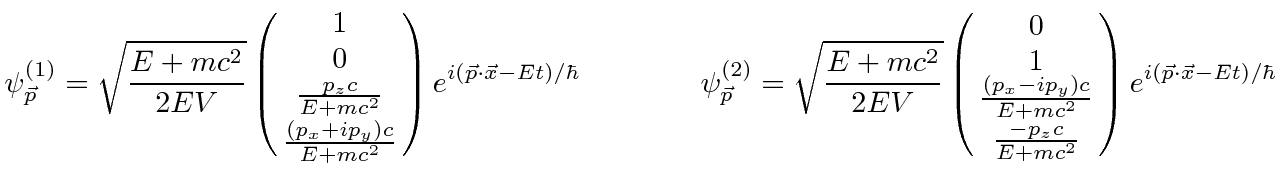
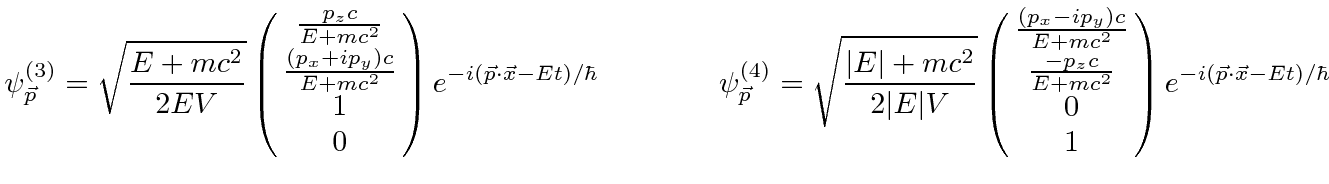
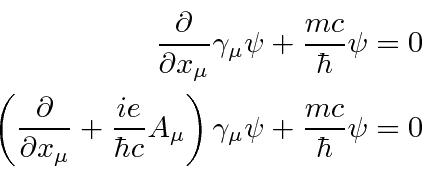
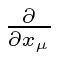 operating on the exponential produces
operating on the exponential produces
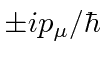 .
If we change the charge on the electron from
.
If we change the charge on the electron from