Next: Equivalence of a Two Up: Dirac Equation Previous: Alternate Labeling of the Contents
We cannot discount the ``negative energy'' solutions since the positive energy solutions alone do not form a complete set. An electron which is localized in space, will have components of its wave function which are ``negative energy''. (The infinite plane wave solutions we have found can be all positive energy.) The more localized the state, the greater the ``negative energy'' content.
One problem of the ``negative energy'' states is that an electron in a positive energy (bound or free) state should be able to emit a photon and make a transition to a ``negative energy'' state. The process could continue giving off an infinite amount of energy. Dirac postulated a solution to this problem. Suppose that all of the ``negative energy'' states are all filled and the Pauli exclusion principle keeps positive energy electrons from making transitions to them.
The positive energies must all be bigger than
![]() and the negative energies must all be less than
and the negative energies must all be less than
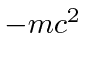 .
There is an energy gap of
.
There is an energy gap of
![]() .
It would be possible for a
``negative energy'' electron to absorb a photon and make a transition to a positive energy state.
The minimum photon energy that could cause this would be
.
It would be possible for a
``negative energy'' electron to absorb a photon and make a transition to a positive energy state.
The minimum photon energy that could cause this would be
![]() .
(Actually to conserve momentum and energy, this must be done near a nucleus (for example)).
A hole would be left behind
in the usual vacuum which has a positive charge relative to the vacuum in which all the ``negative energy'' states are filled.
This hole has all the properties of a positron.
It has positive energy relative to the vacuum.
It has momentum and spin in the opposite direction of the empty ``negative energy'' state.
The process of moving an electron to a positive energy state is like pair creation;
it produces both an electron and a hole which we interpret as a positron.
The discovery of the positron gave a great deal of support to the hole theory.
.
(Actually to conserve momentum and energy, this must be done near a nucleus (for example)).
A hole would be left behind
in the usual vacuum which has a positive charge relative to the vacuum in which all the ``negative energy'' states are filled.
This hole has all the properties of a positron.
It has positive energy relative to the vacuum.
It has momentum and spin in the opposite direction of the empty ``negative energy'' state.
The process of moving an electron to a positive energy state is like pair creation;
it produces both an electron and a hole which we interpret as a positron.
The discovery of the positron gave a great deal of support to the hole theory.
The idea of an infinite sea of ``negative energy'' electrons is a strange one. What about all that charge and negative energy? Why is there an asymmetry in the vacuum between negative and positive energy when Dirac's equation is symmetric? (We could also have said that positrons have positive energy and there is an infinite sea of electrons in negative energy states.) This is probably not the right answer but it has many elements of truth in it. It also gives the right result for some simple calculations. When the Dirac field is quantized, we will no longer need the infinite ``negative energy'' sea, but electrons and positrons will behave as if it were there.
Another way to look at the ``negative energy'' solution is as a positive energy solution moving backward in time.
This makes the same change of the sign in the exponential.
The particle would move in the opposite direction of its momentum.
It would also behave as if it had the opposite charge.
We might just relabel
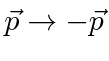 since these solutions go in the opposite direction anyway
and change the sign of
since these solutions go in the opposite direction anyway
and change the sign of
![]() so that it is positive.
The exponential would be then change to
so that it is positive.
The exponential would be then change to
Jim Branson 2013-04-22