Next: Relativistic Covariance Up: Dirac Equation Previous: ``Negative Energy'' Solutions: Hole Contents
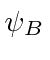 depending on it) is equivalent to the Dirac theory.
It has a second order equation and separate negative and positive energy solutions.
As we saw in the non-relativistic limit, the normalization condition is a bit unnatural in the two component theory.
The normalization correction would be very large for the ``negative energy'' states if we continued to use
depending on it) is equivalent to the Dirac theory.
It has a second order equation and separate negative and positive energy solutions.
As we saw in the non-relativistic limit, the normalization condition is a bit unnatural in the two component theory.
The normalization correction would be very large for the ``negative energy'' states if we continued to use
Even though it is a second order differential equation, we only need to specify the wave function and whether it is negative or positive energy to do the time development. The Dirac theory has many advantages in terms of notation and ease of forming Lorentz covariant objects. A decision must be made when we determine how many independent fields there are.