Dirac Particle at Rest

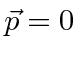To study this further, lets take the simple case of the free particle at rest. This is just the $\vec{p}=0$ case of the the solution above so the energy equation gives $E=\pm mc^2$. The Dirac equation can now be used.

$$\begin{eqnarray*} \left(\gamma_\mu{\partial\over\partial x_\mu}+{mc\over\hbar}\r... ...ma_4\psi_0={mc\over\hbar}\psi_0 \\ \gamma_4\psi_0=\pm\psi_0 \\ \end{eqnarray*}$$

This is a very simple equation, putting conditions on the spinor $\psi_0$.

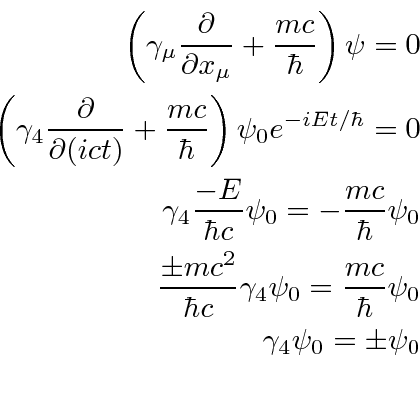
Lets take the case of positive energy first.

$$\begin{eqnarray*} \gamma_4\psi_0=+\psi_0 \\ \pmatrix{1 & 0 & 0 & 0 \cr 0 & 1 & ... ...} \\ B_1=B_2=0 \\ \psi_0=\pmatrix{A_1\cr A_2\cr 0\cr 0\cr} \\ \end{eqnarray*}$$

We see that the positive energy solutions, for a free particle at rest, are described by the upper two component spinor. what we have called $\psi_A$. We are free to choose each component of that spinor independently. For now, lets assume that the two components can be used to designate the spin up and spin down states according to some quantization axis.

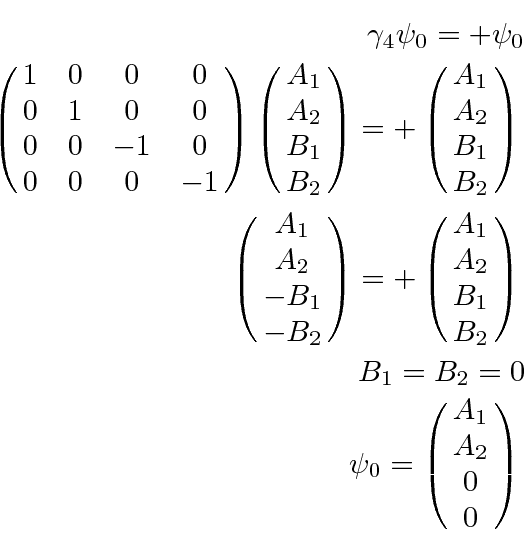
For the ``negative energy solutions'' we have.

$$\begin{eqnarray*} \pmatrix{1 & 0 & 0 & 0 \cr 0 & 1 & 0 & 0 \cr 0 & 0 & -1 & 0 \c... ...} \\ A_1=A_2=0 \\ \psi_0=\pmatrix{0\cr 0\cr B_1\cr B_2\cr} \\ \end{eqnarray*}$$

We can describe two spin states for the ``negative energy solutions''.

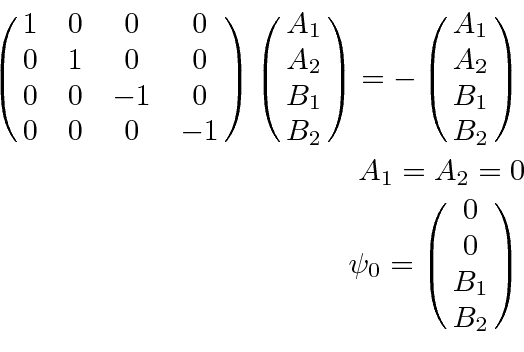
Recall that we have demonstrated that the first two components of $\psi$ are large compared to the other two for a non-relativistic electron solution and that the first two components, $\psi_A$, can be used as the two component spinor in the Schrödinger equation (with a normalization factor). Lets identify the first component as spin up along the z axis and the second as spin down. (We do still have a choice of quantization axis.) Define a 4 by 4 matrix which gives the z component of the spin.

$$\begin{eqnarray*} \Sigma_z&=&{1\over 2i}(\gamma_1\gamma_2-\gamma_2\gamma_1) \\ ... ...a_y] \cr} \\ &=&\pmatrix{\sigma_z & 0 \cr 0 & \sigma_z \cr} \\ \end{eqnarray*}$$

With this matrix defining the spin, the third component is the one with spin up along the z direction for the ``negative energy solutions''. We could also define 4 by 4 matrices for the x and y components of spin by using cyclic permutations of the above.

So the four normalized solutions for a Dirac particle at rest are.

$$\psi^{(1)}=\psi_{E=+mc^2,+\hbar/2}={1\over\... ...\hbar/2}={1\over\sqrt{V}}\pmatrix{0\cr 1\cr 0\cr 0\cr}e^{-imc^2t/\hbar}$$

$$\psi^{(3)}=\psi_{E=-mc^2,+\hbar/2}={1\over\sq... ...\hbar/2}={1\over\sqrt{V}}\pmatrix{0\cr 0\cr 0\cr 1\cr}e^{+imc^2t/\hbar}$$

The first and third have spin up while the second and fourth have spin down. The first and second are positive energy solutions while the third and fourth are ``negative energy solutions'', which we still need to understand.