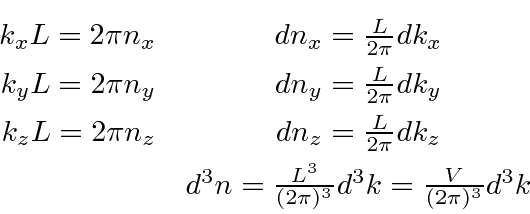We have some experience with calculating the
number of states for fermions in a 3D box.
For the box we had boundary conditions that the wavefunction go to zero at the wall of the box.
Now we wish to know how many photon states are in a region of phase space centered on the wave vector
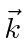 with
(small) volume in k-space of
with
(small) volume in k-space of
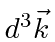 .
(Remember
.
(Remember
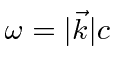 for light.)
We will assume for the sake of calculation that the photons are confined to a cubic volume in position space of
for light.)
We will assume for the sake of calculation that the photons are confined to a cubic volume in position space of
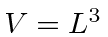 and impose periodic boundary conditions on our fields.
(Really we could require the fields to be zero on the boundaries of the box by choosing a sine wave. The PBC are
equivalent to this but allow us to deal with single exponentials instead of real functions.)
Our final result, the decay rate, will be independent of volume so we can let the volume go to infinity.
and impose periodic boundary conditions on our fields.
(Really we could require the fields to be zero on the boundaries of the box by choosing a sine wave. The PBC are
equivalent to this but allow us to deal with single exponentials instead of real functions.)
Our final result, the decay rate, will be independent of volume so we can let the volume go to infinity.
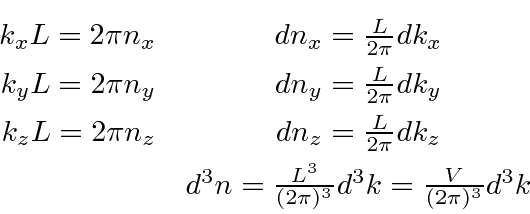
That was easy.
We will use this phase space formula for decays of atoms emitting a photon.
A
more general phase space formula
based on our calculation can be used with more than one free particle in the final state.
(In fact, even our simple case, the atom recoils in the final state, however, its momentum is fixed due to momentum conservation.)
Jim Branson
2013-04-22
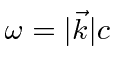 for light.)
We will assume for the sake of calculation that the photons are confined to a cubic volume in position space of
for light.)
We will assume for the sake of calculation that the photons are confined to a cubic volume in position space of