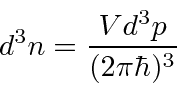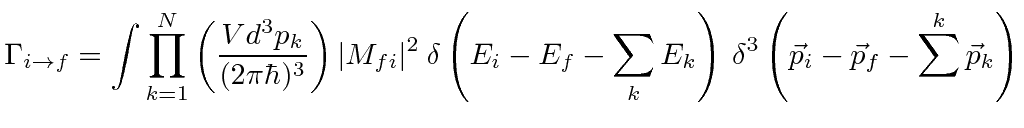General Phase Space Formula
If there are
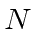 particles in the final state, we must consider the number of states available for
each one.
Our phase space calculation for photons was correct even for particles with masses.
particles in the final state, we must consider the number of states available for
each one.
Our phase space calculation for photons was correct even for particles with masses.
Using Fermi's Golden Rule as a basis, we include the general phase space formula into our formula for transition rates.
In our case, for example, of an atom decaying by the emission of one photon, we have two particles in the final state and the
delta function of momentum conservation will do one of the 3D integrals getting us back to the same result.
We have not bothered to deal with the free particle wave function of the recoiling atom, which will give the factor of
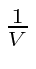 to cancel the
to cancel the
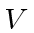 in the phase space for the atom.
in the phase space for the atom.
Jim Branson
2013-04-22