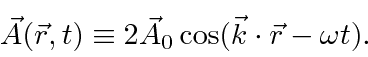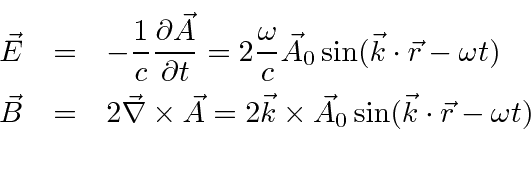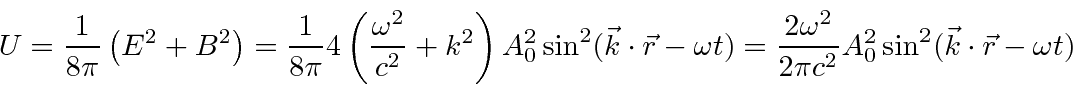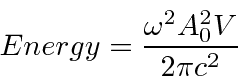Energy in Field for a Given Vector Potential

We have the vector potential

$$\bgroup\color{black} \vec{A}(\vec{r},t)\equiv 2\vec{A}_0\cos(\vec{k}\cdot\vec{r}-\omega t). \egroup$$

First find the fields.

$$\begin{eqnarray*} \vec{E}&=&-{1\over c}{\partial \vec{A}\over \partial t}=2{\ome... ...A}=2\vec{k}\times\vec{A}_0\sin(\vec{k}\cdot\vec{r}-\omega t) \\ \end{eqnarray*}$$

Note that, for an EM wave, the vector potential is transverse to the wave vector. The energy density in the field is

$$\bgroup\color{black} U={1\over 8\pi}\left(E^2+B^2\right)={1\o... ...over 2\pi c^2}A_0^2\sin^2(\vec{k}\cdot\vec{r}-\omega t) \egroup$$

Averaging the sine square gives one half, so, the energy in a volume 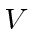$V$ is

$$\bgroup\color{black} Energy={\omega^2A_0^2V\over 2\pi c^2} \egroup$$