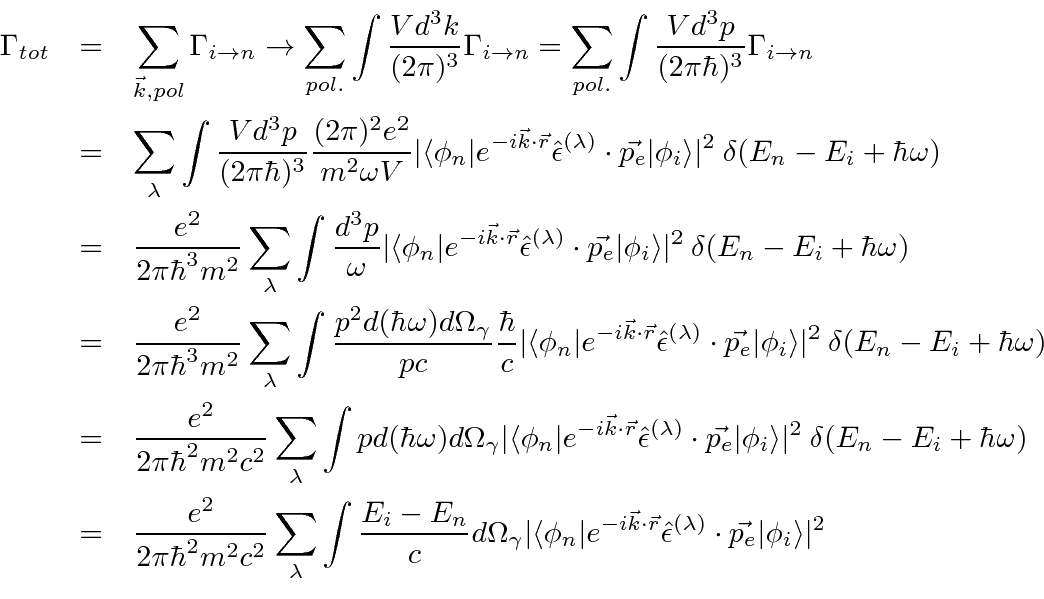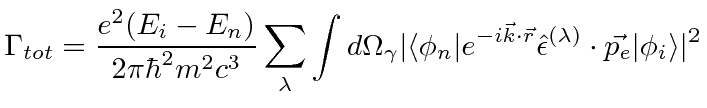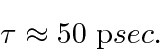Total Decay Rate Using Phase Space

Now we are ready to sum over final (photon) states to get the total transition rate. Since both the momentum of the photon and the electron show up in this equation, we will label the electron's momentum to avoid confusion.

$$\begin{eqnarray*} \Gamma_{tot}&=&\sum\limits_{\vec{k},pol}\Gamma_{i\rightarrow n... ...\epsilon}^{(\lambda)}\cdot\vec{p_e}\vert\phi_i\rangle\vert^2 \\ \end{eqnarray*}$$

$$\Gamma_{tot}={e^2(E_i-E_n)\over 2\pi\hbar^2 m... ...vec{r}}\hat{\epsilon}^{(\lambda)}\cdot\vec{p_e}\vert\phi_i\rangle\vert^2$$

This is the general formula for the decay rate emitting one photon. Depending on the problem, we may also need to sum over final states of the atom. The two polarizations are transverse to the photon direction, so they must vary inside the integral.

A quick estimate of the decay rate of an atom gives

$$\bgroup\color{black} \tau\approx 50 {\mathrm psec.} \egroup$$