Decay Rates for the Emission of Photons

Our expression for the decay rate of an initial state $\phi_i$ into some particular final state $\phi_n$ is

$$\bgroup\color{black} \Gamma_{i\rightarrow n}= {2\pi V_{ni}^2\over \hbar}\:\delta(E_n-E_i+\hbar\omega). \egroup$$

The delta function reminds us that we will have to integrate over final states to get a sensible answer. Nevertheless, we proceed to include the matrix element of the perturbing potential.

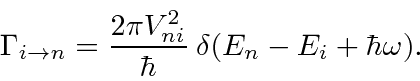
Taking out the harmonic time dependence (to the delta function) as before, we have the matrix element of the perturbing potential.

$$\bgroup\color{black} V_{ni}=\langle\phi_n\vert{e\over mc}\vec... ...dot\vec{r}}\hat{\epsilon}\cdot\vec{p}\vert\phi_i\rangle \egroup$$

We just put these together to get

$$\begin{eqnarray*} \Gamma_{i\rightarrow n}&=&{2\pi\over \hbar}{e^2\over m^2c^2}\l... ...vec{p}\vert\phi_i\rangle\vert^2\:\delta(E_n-E_i+\hbar\omega) \\ \end{eqnarray*}$$

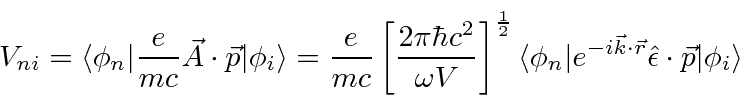
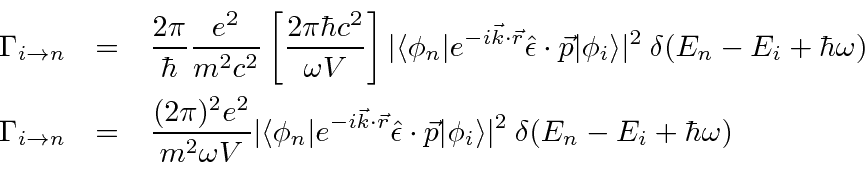
We must sum (or integrate) over final states. The states are distinguishable so we add the decay rates, not the amplitudes. We will integrate over photon energies and directions, with the aid of the delta function. We will sum over photon polarizations. We will sum over the final atomic states when that is applicable. All of this is quite doable. Our first step is to understand the number of states of photons as Plank (and even Rayleigh) did to get the Black Body formulas.