Next: The Periodic Table Up: Atomic Physics Previous: The Hartree Equations Contents
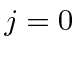 states for the closed shells.
As we add valence electrons we follow Hund's rules to determine the ground state.
We get a great simplification by treating nearly closed shells as a closed shell plus
positively charged, spin
states for the closed shells.
As we add valence electrons we follow Hund's rules to determine the ground state.
We get a great simplification by treating nearly closed shells as a closed shell plus
positively charged, spin
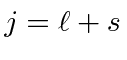 otherwise pick the lowest
otherwise pick the lowest 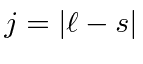 .
.
This method of adding up all the spins and all the Ls, is called LS or Russel-Saunders coupling.
This method and these rule are quite good until the electrons become relativistic in heavy atoms and
spin-orbit effects become comparable to the electron repulsion (arond Z=40).
We choose the states in which the total
![]() and the total
and the total
![]() are good quantum numbers
are best for minimizing the overlap of electrons, and hence the positive contribution to the energy.
are good quantum numbers
are best for minimizing the overlap of electrons, and hence the positive contribution to the energy.
For very heavy atoms, we add the total angular momentum from each electron first then add up the Js. This is called j-j coupling. For heavy atoms, electrons are relativistic and the spin-orbit interaction becomes more important than the effect of electron repulsion. Thus we need to use states in which the total angular momentum of each electron is a good quantum number.
We can understand Hund's rules to some extent.
The maximum spin state is symmetric under interchange,
requiring an antisymmetric spatial wavefunction which has a lower energy
as we showed for Helium.
We have not demonstated it, but, the larger the total
![]() the more lobes there are in the
overall electron wavefunction and the lower the effect of electron repulsion.
Now the spin orbit interaction comes into play.
For electrons with their negative charge, larger
the more lobes there are in the
overall electron wavefunction and the lower the effect of electron repulsion.
Now the spin orbit interaction comes into play.
For electrons with their negative charge, larger
![]() increases the energy.
The reverse is true for holes which have an effective postive charge.
increases the energy.
The reverse is true for holes which have an effective postive charge.
A simpler set of rules has been developed for chemists,
who can't understand addition of angular momentum.
It is based on the same principles.
The only way to have a totally antisymmetric state is to have no two electrons in the
same state.
We use the same kind of trick we used to get a feel for addition of angular momentum;
that is, we look at the maximum z component we can get consistent with the Pauli principle.
Make a table with space for each of the different
![]() states in the outer shell.
We can put two electrons into each space, one with spin up and one with spin down.
Fill the table with the number of valence electrons according to the following rules.
states in the outer shell.
We can put two electrons into each space, one with spin up and one with spin down.
Fill the table with the number of valence electrons according to the following rules.
* Example:
The Boron ground State.*
* Example:
The Carbon ground State.*
* Example:
The Nitrogen ground State.*
* Example:
The Oxygen ground State.*
Jim Branson 2013-04-22