Next: Nitrogen Ground State Up: Examples Previous: Boron Ground State Contents
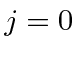 as a base.
It has two valence 2P electrons.
Hund's first rule , maximum total
as a base.
It has two valence 2P electrons.
Hund's first rule , maximum total
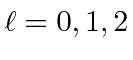 .
The maximum state is symmetric, the next antisymmetric, and the
.
The maximum state is symmetric, the next antisymmetric, and the
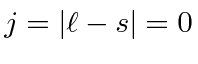 .
So the ground state is
.
So the ground state is
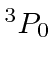 .
The simpler way works with a table.
.
The simpler way works with a table.
|
|
e |
| 1 |
|
| 0 |
|
| -1 | |
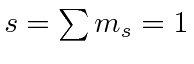 |
|
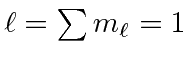 |
|
We can take a look at the excited states of carbon to get an appreciation of
Hund's rules.
The following chart shows the states of a carbon atom.
For most states, a basis of
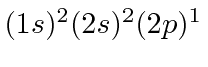 is assumed and the state of the
sixth electron is given.
Some states have other excited electrons and are indicated by a superscript.
Different
is assumed and the state of the
sixth electron is given.
Some states have other excited electrons and are indicated by a superscript.
Different
![]() states are not shown since the splitting is small.
Electric dipole transitions are shown changing
states are not shown since the splitting is small.
Electric dipole transitions are shown changing
![]() by one unit.
by one unit.
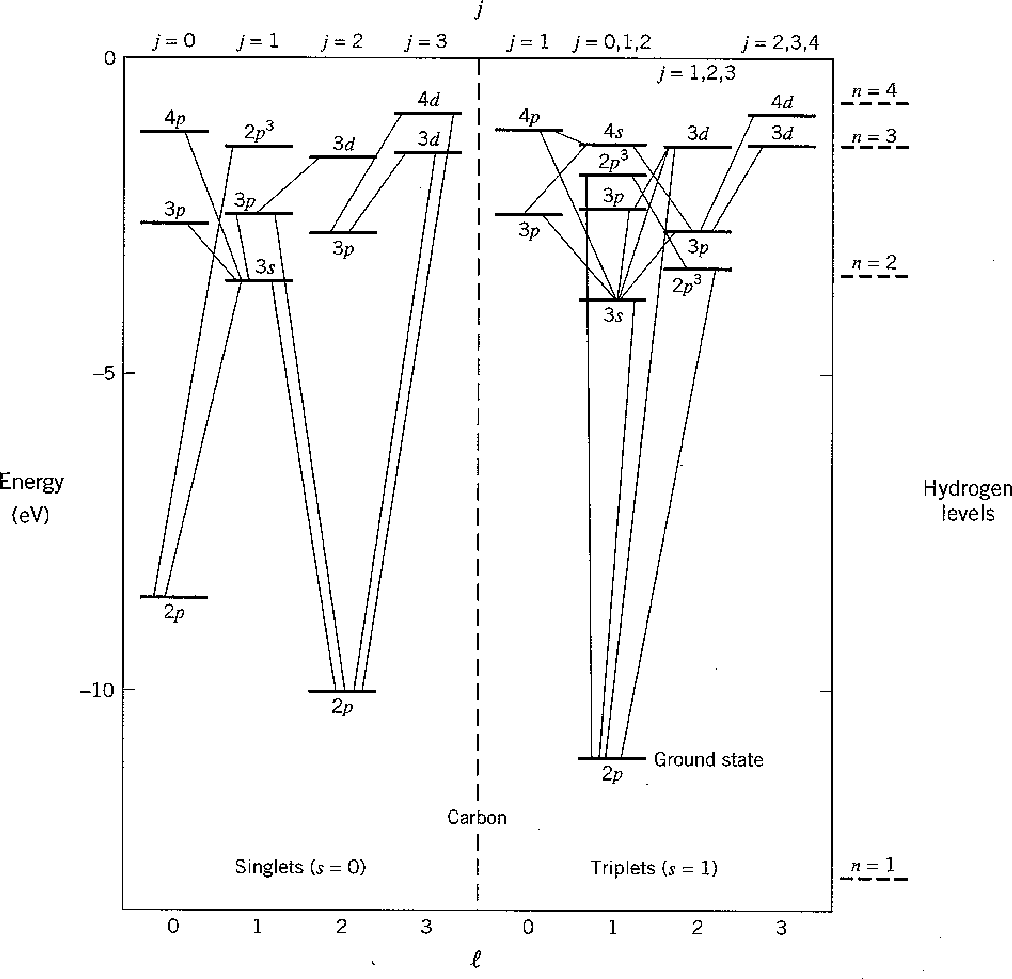
The ground state has
![]() and
and
![]() as we predicted.
Other states labeled
as we predicted.
Other states labeled
![]() are the ones that Hund's first two rules
determined to be of higher energy.
They are both spin singlets so its the symmetry of the space wavefunction
that is making the difference here.
are the ones that Hund's first two rules
determined to be of higher energy.
They are both spin singlets so its the symmetry of the space wavefunction
that is making the difference here.
Jim Branson 2013-04-22