Next: Oxygen Ground State Up: Examples Previous: Carbon Ground State Contents
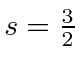 .
This is again the symmetric spin state so we'll need to make the space state antisymmetric.
We now have the truly nasty problem of figuring out which total
.
This is again the symmetric spin state so we'll need to make the space state antisymmetric.
We now have the truly nasty problem of figuring out which total
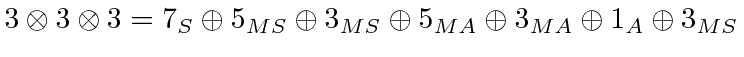 .
Here MS means mixed symmetric.
That is; it is symmetric under the interchange of two of the electrons but not
with the third.
Remember, adding two P states together, we get total
.
Here MS means mixed symmetric.
That is; it is symmetric under the interchange of two of the electrons but not
with the third.
Remember, adding two P states together, we get total
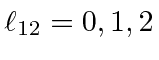 .
Adding another P state to each of these gives total
.
Adding another P state to each of these gives total
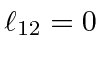 ,
,
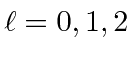 for
for
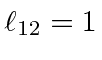 ,
and
,
and
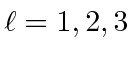 for
for
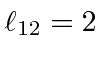 .
Hund's second rule, maximum
.
Hund's second rule, maximum
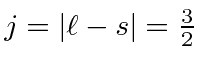 .
So the ground state is
.
So the ground state is
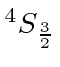 .
.
|
|
e |
| 1 |
|
| 0 |
|
| -1 |
|
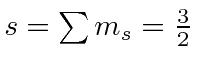 |
|
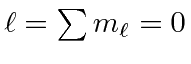 |
|
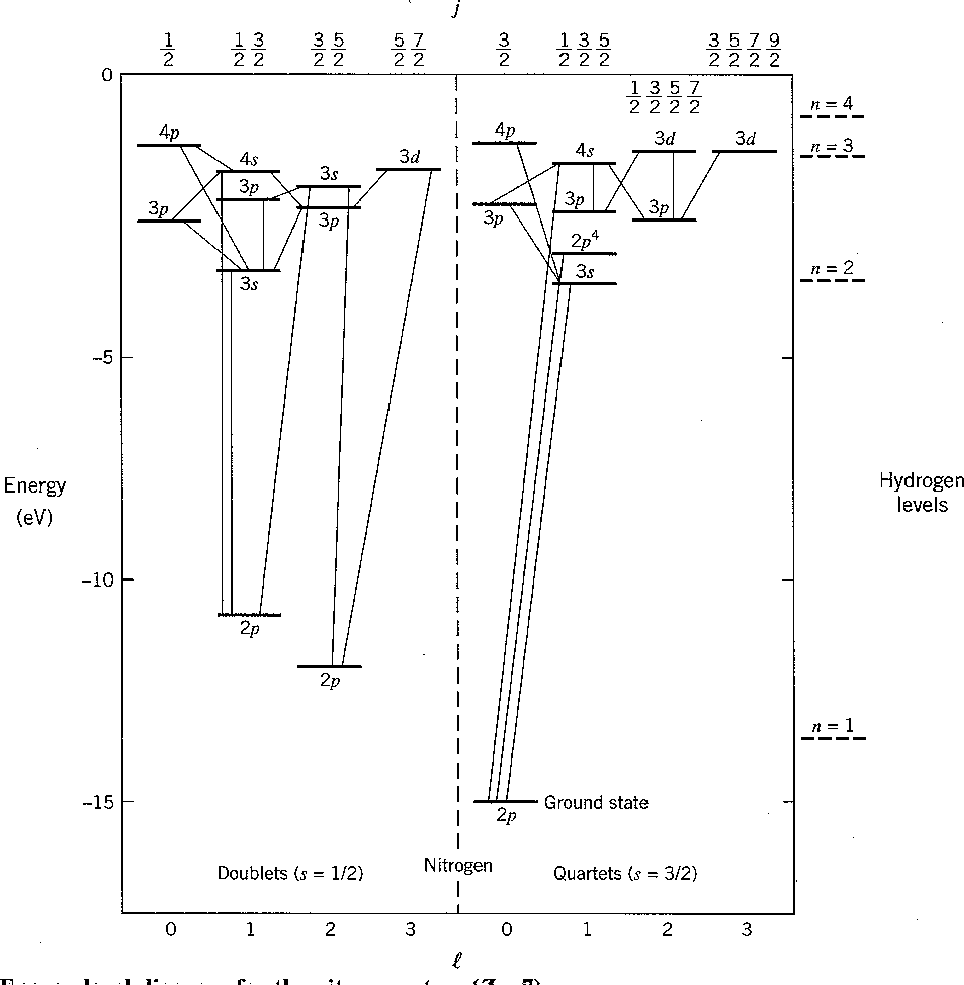
The chart of nitrogen states is similar to the chart in the last section. Note that the chart method is clearly easier to use in this case. Our prediction of the ground state is again correct and a few space symmetric states end up a few eV higher than the ground state.
Jim Branson 2013-04-22