Hydrogen Fine Structure

The basic hydrogen problem we have solved has the following Hamiltonian.

$$\bgroup\color{black} H_0 = {p^2\over {2\mu}} - {Ze^2\over r} \egroup$$

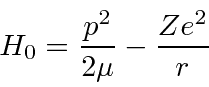
To this simple Coulomb problem, we will add several corrections:

1. The relativistic correction to the electron's kinetic energy.
2. The Spin-Orbit correction.
3. The ``Darwin Term'' correction to s states from Dirac eq.
4. The ((anomalouus) Zeeman) effect of an external magnetic field.

Correction (1) comes from relativity. The electron's velocity in hydrogen is of order $\alpha c$. It is not very relativistic but a small correction is in order. By calculating the next order relativistic correction to the kinetic energy we find the additional term in the Hamiltonian

$$\bgroup\color{black} H_1=-{1\over 8}{p^4_e \over {m^3 c^2}}.\egroup$$

Our energy eigenstates are not eigenfunctions of this operator so we will have to treat it as a perturbation.

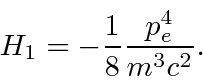
We can estimate the size of this correction compared to the Hydrogen binding energy by taking the ratio to the Hydrogen kinetic energy. (Remember that, in the hydrogen ground state, $\left<{p^2\over 2m}\right>=-E={1\over 2}\alpha^2mc^2$.)

$$\bgroup\color{black} {p^4 \over {8 m^3 c^2}} \div {p^2 \over ... ...c^2}} = {(p^2/2m) \over {2mc^2}} = {1\over 4}\alpha ^2 \egroup$$

Like all the fine structure corrections, this is down by a factor of order $\alpha^2$ from the Hydrogen binding energy.

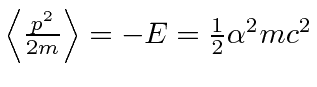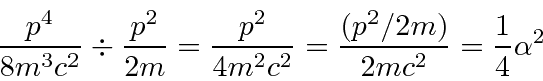
The second term, due to Spin-Orbit interactions, is harder to derive correctly. We understand the basis for this term. The magnetic moment from the electron's spin interacts with the B field produced by the current seen in the electron's rest frame from the circulating proton.

$$\bgroup\color{black} H_2 = -\vec\mu_e \cdot\vec B \egroup$$

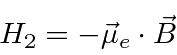
We can derive B from a Lorentz transformation of the E field of a static proton (We must also add in the Thomas Precession which we will not try to understand here).

$$\bgroup\color{black} H_2 = {1\over 2}{ge^2\over {2m^2c^2r^3}}\vec L \cdot\vec S \egroup$$

This will be of the same order as the relativistic correction.

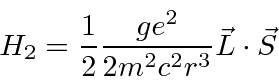
Now we compute the relativity correction in first order perturbation theory .

$$\bgroup\color{black} \left< \psi_{nlm}\left\vert H_1\right\ve... ...mc^2}} \left[ 3 - {4n \over{\ell + {1\over 2}}} \right] \egroup$$

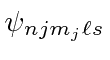The result depends on $\ell$ and $n$, but not on $m_\ell$ or $j$. This means that we could use either the $\psi_{njm_j\ell s}$ or the $\psi_{n\ell m_\ell sm_s}$ to calculate the effect of $H_1$. We will need to use the $\psi_{njm_j\ell s}$ to add in the spin-orbit.

The first order perturbation energy shift from the spin orbit correction is calculated for the states of definite $j$.

$$\bgroup\color{black}\left<\psi_{nlm}\left\vert H_2\right\vert... ...l(\ell+1)-s(s+1)\right]\left<{1\over{r^3}}\right>_{nlm} \egroup$$

$$\bgroup\color{black} = \left({g\over 2}\right) {{E^{(0)}_n}^2... ...ad \matrix{ j=\ell + {1\over 2} \cr j=\ell -{1\over 2} }\egroup$$

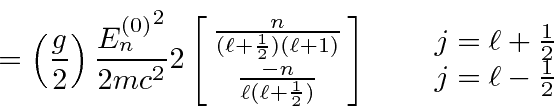
Actually, the $\vec L\cdot\vec S$ term should give 0 for $\ell=0$! In the above calculation there is an ${\ell\over\ell}$ factor which makes the result for $\ell=0$ undefined. There is an additional Dirac Equation contribution called the ``Darwin term'' which is important for $\ell=0$ and surprisingly makes the above calculation right, even for $\ell=0$!

We will now add these three fine structure corrections together for states of definite $j$. We start with a formula which has slightly different forms for $j=\ell\pm{1\over 2}$.

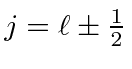$$\bgroup\color{black}E_{njm_j\ell s}=E^{(0)}_n + {{E^{(0)}_n}^... ...{\ell(\ell+{1\over 2})}} } \right\}^{(+)}_{(-)}\right]\egroup$$

$$\bgroup\color{black}E_{njm_j\ell s} =E^{(0)}_n + {{E^{(0)}_n}... ...ll+1}} \cr 4+{2\over\ell}} \right\}^{(+)}_{(-)}\right]\egroup$$

$$\bgroup\color{black}E_{njm_j\ell s} =E^{(0)}_n + {{E^{(0)}_n}... ...{2\over{j+{1\over 2}}}\over{\ell+{1\over 2}} } \right]\egroup$$

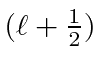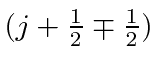We can write $(\ell+{1\over 2})$ as $(j+{1\over 2}\mp{1\over 2})$, so that

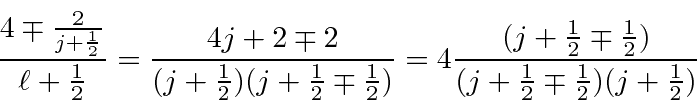
$$\bgroup\color{black}{ 4\mp{2\over{j+{1\over 2}}}\over{\ell+{1... ...2}) \over {(j+{1\over 2}\mp{1\over 2})(j+{1\over 2}) }} \egroup$$

and we get a nice cancellation giving us a simple formula.

$E_{nlm} = E^{(0)}_n + {{E^{(0)}_n}^2 \over {2mc^2}} \left[3 - {4n\over{j+{1\over 2}}}\right]$

This is independent of $\ell$ so the states of different total angular momentum split in energy but there is still a good deal of degeneracy.

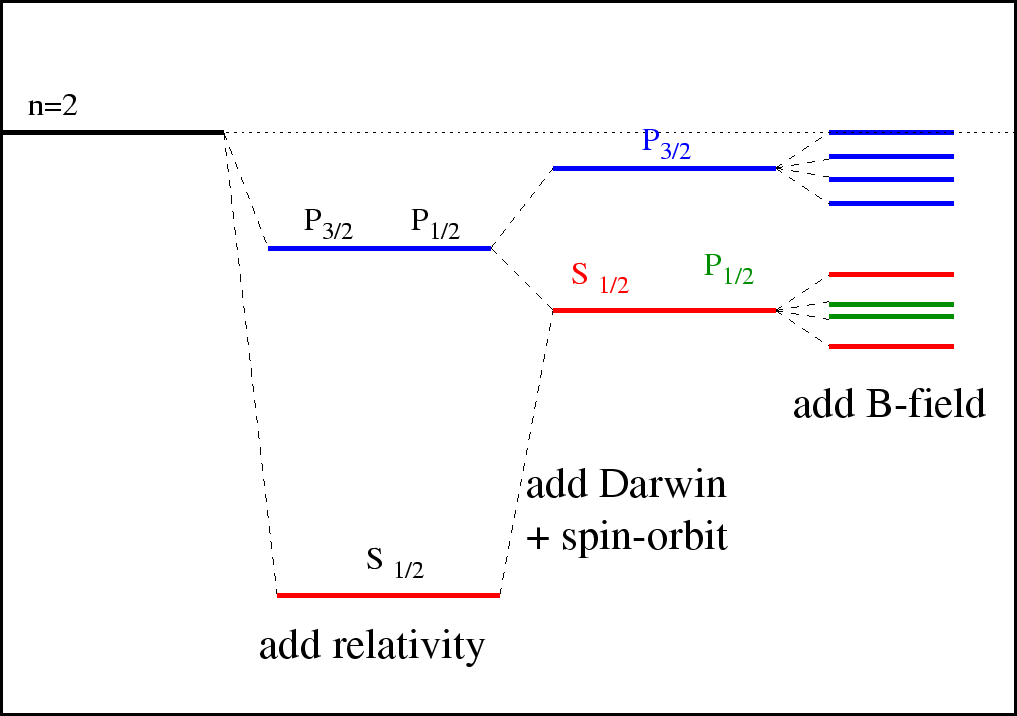
We have calculated the fine structure effects in Hydrogen. There are, of course, other, smaller corrections to the energies. A correction from field theory, the Lamb Shift, causes states of different $\ell$ to shift apart slightly. Nevertheless, the states of definite total angular momentum are the energy eigenstates until we somehow break spherical symmetry.