Next: Perturbation Calculation for H2 Up: Derivations and Computations Previous: The Spin-Orbit Correction Contents
Rewriting
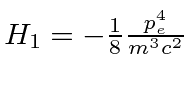 as
as
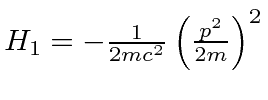 we calculate the energy shift for a state
we calculate the energy shift for a state
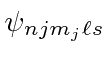 .
While there is no spin involved here, we will need to use these states for the spin-orbit interaction
.
While there is no spin involved here, we will need to use these states for the spin-orbit interaction
![\begin{eqnarray*}
\left< \psi_{njm_j\ell s}\left\vert H_1\right\vert \psi_{njm_j...
...er r}\right>_{n}
+ e^4\left<{1\over {r^2}}\right>_{nl} \right]
\end{eqnarray*}](img3111.png)
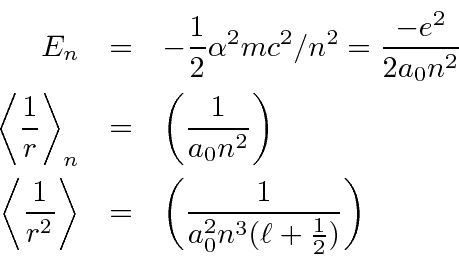
![\begin{eqnarray*}
\left< \psi_{njm_j\ell s}\left\vert H_1\right\vert \psi_{njm_j...
... \over {2mc^2}} \left[ 3 - {4n \over{\ell + {1\over 2}}} \right]
\end{eqnarray*}](img3113.png)
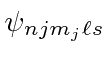 , so that we can combine this correction
with the spin-orbit correction.
, so that we can combine this correction
with the spin-orbit correction.