Next: Perturbation Calculation for Relativistic Up: Derivations and Computations Previous: The Relativistic Correction Contents
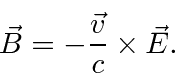
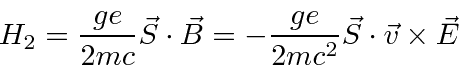
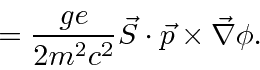
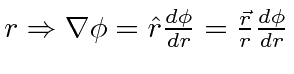
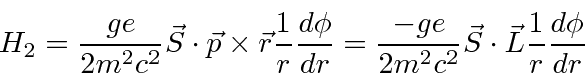
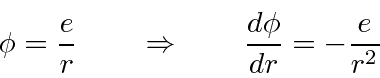
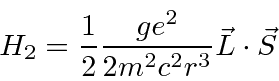
Note that this was just a classical calculation which we will apply to quantum states later.
It is correct for the EM forces, but,
the electron is actually in a rotating system which gives an additional
![]() term
(not from the B field!).
This term is 1/2 the size and of opposite sign.
We have already included this factor of 2 in the answer given above.
term
(not from the B field!).
This term is 1/2 the size and of opposite sign.
We have already included this factor of 2 in the answer given above.
Recall that
![\begin{displaymath}\bgroup\color{black} H_2 \propto \vec L \cdot\vec S = {1\over 2}\left[J^2 - L^2 - S^2\right] \egroup\end{displaymath}](img3108.png)
Jim Branson 2013-04-22