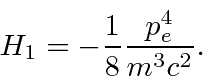Next: The Spin-Orbit Correction Up: Derivations and Computations Previous: Derivations and Computations Contents
Moving from the non-relativistic formula for the energy of an electron
to the relativistic formula we make the change
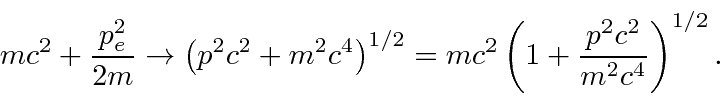
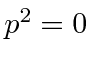 , we find
, we find
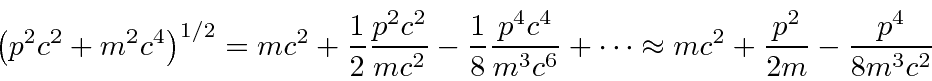
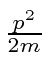 was just the lowest order correction to
was just the lowest order correction to
What about the ``reduced mass problem''? The proton is very non-relativistic so only the electron term is important and the reduced mass is very close to the electron mass. We can therefore neglect the small correction to the small correction and use