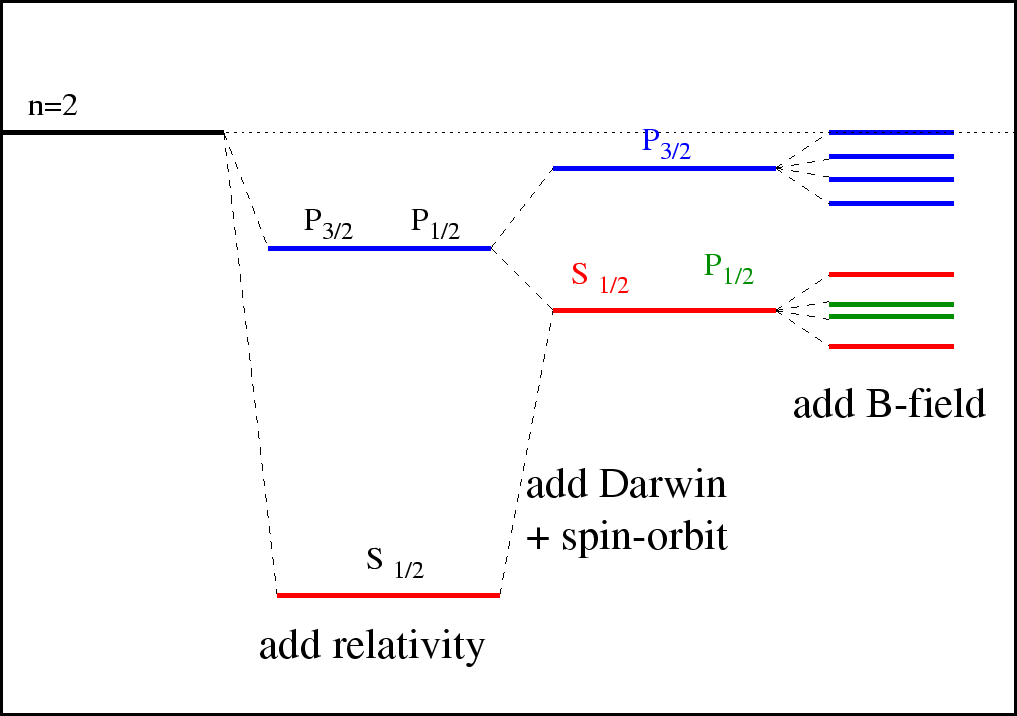
Next: Examples Up: Fine Structure in Hydrogen Previous: Hydrogen Fine Structure Contents
One way to break the spherical symmetry is to apply an external B field.
Lets assume that the field is weak enough that the energy shifts due to it are
smaller than the fine structure corrections.
Our Hamiltonian can now be written as
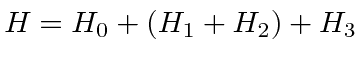 , where
, where
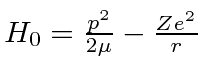 is the normal Hydrogen problem,
is the normal Hydrogen problem,
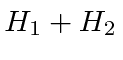 is the fine structure correction, and
is the fine structure correction, and
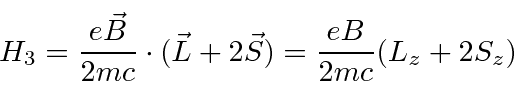
We now run into a problem because
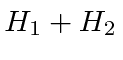 picks eigenstates of
picks eigenstates of
![]() and
and
![]() while
while
![]() picks eigenstates of
picks eigenstates of
![]() and
and
![]() .
In the weak field limit, we can do perturbation theory using the states of
definite
.
In the weak field limit, we can do perturbation theory using the states of
definite
![]() .
A direct calculation
of the Anomalous Zeeman Effect gives the energy
shifts in a weak B field.
.
A direct calculation
of the Anomalous Zeeman Effect gives the energy
shifts in a weak B field.
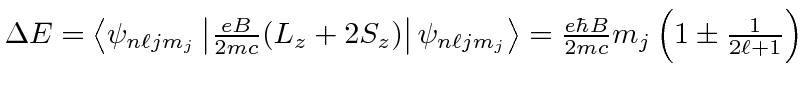 |
![\begin{displaymath}\bgroup\color{black}E_{njm_j\ell s}=-{1\over 2}\alpha^2mc^2\l...
...^3}\left[{1\over j+{1\over 2}}-{3\over 4n}\right]\right)\egroup\end{displaymath}](img3095.png)
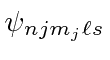 .
All the states can be detected spectroscopically.
.
All the states can be detected spectroscopically.
The factor
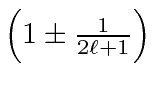 is known as the Lande
is known as the Lande ![]() Factorbecause the state splits as if it had this gyromagnetic ratio.
We know that it is in fact a combination of the orbital and spin g factors in a state of
definite
Factorbecause the state splits as if it had this gyromagnetic ratio.
We know that it is in fact a combination of the orbital and spin g factors in a state of
definite
![]() .
.
In the strong field limit we could use states of definite
![]() and
and
![]() and
calculate the effects of the fine structure,
and
calculate the effects of the fine structure,
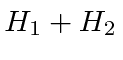 , as a correction.
We will not calculate this here.
If the field is very strong, we can neglect the fine structure entirely.
Then the calculation is easy.
, as a correction.
We will not calculate this here.
If the field is very strong, we can neglect the fine structure entirely.
Then the calculation is easy.
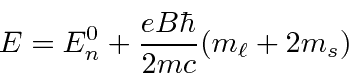
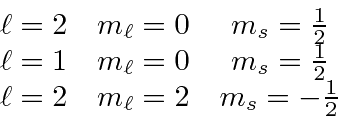
Jim Branson 2013-04-22