Next: Degenerate State Perturbation Theory Up: Time Independent Perturbation Theory Previous: Time Independent Perturbation Theory Contents
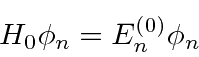
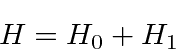
The Schrödinger equation for the full problem is
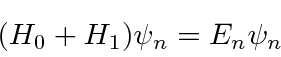
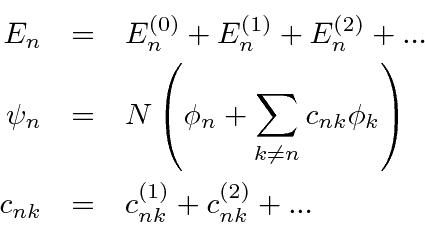
By solving the Schrödinger equation at each order of the perturbation series, we compute the corrections to the energies and eigenfunctions.
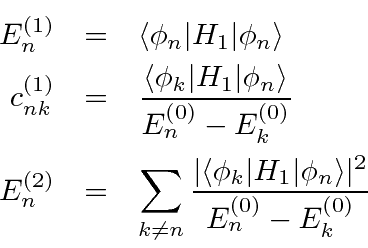
So the first order correction to the energy of the
![]() eigenstate,
eigenstate,
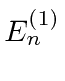 ,
is just the expectation value of the perturbation in the unperturbed state.
The first order admixture of
,
is just the expectation value of the perturbation in the unperturbed state.
The first order admixture of
![]() in
in
![]() ,
,
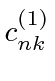 , depends on a matrix element and the energy
difference between states.
The second order correction to the energy,
, depends on a matrix element and the energy
difference between states.
The second order correction to the energy,
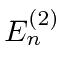 , has a similar dependence.
Note that the higher order corrections may not be small if states are nearby in energy.
, has a similar dependence.
Note that the higher order corrections may not be small if states are nearby in energy.
The application of the first order perturbation equations is quite simple in principal. The actual calculation of the matrix elements depends greatly on the problem being solved.
* Example:
H.O. with anharmonic perturbation (![]() ).*
).*
Sometimes the first order correction to the energy is zero. Then we will need to use
the second order term
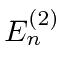 to estimate the correction. This is true when we apply
an electric field to a hydrogen atom.
to estimate the correction. This is true when we apply
an electric field to a hydrogen atom.
* Example:
Hydrogen Atom in a E-field, the Stark Effect.*
We will exercise the use of perturbation theory in section 23 when we compute the fine structure, and other effects in Hydrogen.
Jim Branson 2013-04-22