H.O. with anharmonic perturbation (
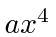 ).
).
We add an anharmonic perturbation to the Harmonic Oscillator problem.
Since this is a symmetric perturbation we expect that it will give a nonzero result in first order
perturbation theory.
First, write x in terms of
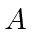 and
and
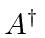 and compute the expectation value as we have
done before.
and compute the expectation value as we have
done before.
Jim Branson
2013-04-22
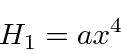
![\begin{eqnarray*}
\Delta E^{(1)}_n
&=& a\langle n \vert x^4\vert n\rangle = {a...
...n(n-1)\right] \\
&=& {3a\hbar^2\over{4m^2\omega^2}}(2n^2+2n+1)
\end{eqnarray*}](img2996.png)