Degenerate State Perturbation Theory

The perturbation expansion has a problem for states very close in energy. The energy difference in the denominators goes to zero and the corrections are no longer small. The series does not converge. We can very effectively solve this problem by treating all the (nearly) degenerate states like we did $\phi_n$ in the regular perturbation expansion. That is, the zeroth order state will be allowed to be an arbitrary linear combination of the degenerate states and the eigenvalue problem will be solved.

Assume that two or more states are (nearly) degenerate. Define $\bgroup\color{black}${\cal N}$\egroup$ to be the set of those nearly degenerate states. Choose a set of basis state in $\bgroup\color{black}${\cal N}$\egroup$ which are orthonormal

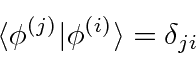
$\begin{displaymath}\bgroup\color{black} \langle\phi^{(j)}\vert\phi^{(i)}\rangle = \delta_{ji} \egroup\end{displaymath}$

where $\bgroup\color{black}$i$\egroup$ and $\bgroup\color{black}$j$\egroup$ are in the set $\bgroup\color{black}${\cal N}$\egroup$ . We will use the indices $\bgroup\color{black}$i$\egroup$ and $\bgroup\color{black}$j$\egroup$ to label the states in $\bgroup\color{black}${\cal N}$\egroup$ .

By looking at the zeroth and first order terms in the Schrödinger equation and dotting it into one of the degenerate states $\bgroup\color{black}$\phi^{(j)}$\egroup$ , we derive the energy equation for first order (nearly) degenerate state perturbation theory

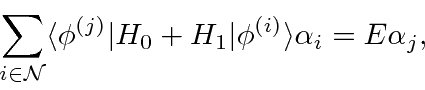
$\begin{displaymath}\bgroup\color{black}\sum\limits_{i\in{\cal N}}\langle\phi^{(j)}\vert H_0+H_1\vert\phi^{(i)}\rangle\alpha_i=E\alpha_j,\egroup\end{displaymath}$

This is an eigenvalue equation with as many solutions as there are degnerate states in our set. audio

We recognize this as simply the (matrix) energy eigenvalue equation limited the list of degenerate states. We solve the equation to get the energy eigenvalues and energy eigenstates, correct to first order.

Written as a matrix, the equation is

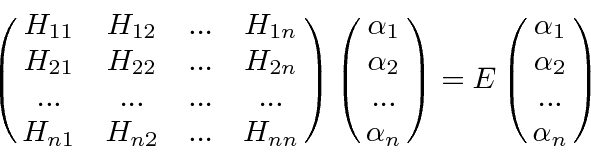
$\begin{displaymath}\bgroup\color{black}\pmatrix{H_{11} & H_{12} &... & H_{1n} \c... ..._n} =E\pmatrix{\alpha_1\cr \alpha_2\cr ...\cr \alpha_n}\egroup\end{displaymath}$

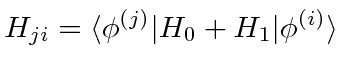where $\bgroup\color{black}$H_{ji}=\langle\phi^{(j)}\vert H_0+H_1\vert\phi^{(i)}\rangle$\egroup$ is the matrix element of the full Hamiltonian. If there are n nearly degenerate states, there are n solutions to this equation.

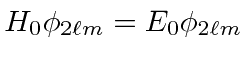The Stark effect for the (principle quantum number) n=2 states of hydrogen requires the use of degenerate state perturbation theory since there are four states with (nearly) the same energies. For our first calculation, we will ignore the hydrogen fine structure and assume that the four states are exactly degenerate, each with unperturbed energy of $\bgroup\color{black}$E_0$\egroup$ . That is $\bgroup\color{black}$H_0\phi_{2\ell m}=E_0\phi_{2\ell m}$\egroup$ . 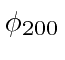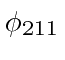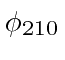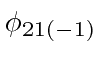The degenerate states $\bgroup\color{black}$\phi_{200}$\egroup$ , $\bgroup\color{black}$\phi_{211}$\egroup$ , $\bgroup\color{black}$\phi_{210}$\egroup$ , and $\bgroup\color{black}$\phi_{21(-1)}$\egroup$ .

* Example: The Stark Effect for n=2 States.*

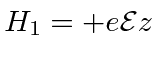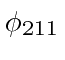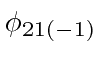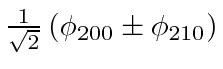The perturbation due to an electric field in the z direction is $\bgroup\color{black}$H_1 = +e{\cal E}z$\egroup$ . 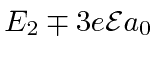The linear combinations that are found to diagonalize the full Hamiltonian in the subspace of degenerate states are: $\bgroup\color{black}$\phi_{211}$\egroup$ , $\bgroup\color{black}$\phi_{21(-1)}$\egroup$ and $\bgroup\color{black}${1\over\sqrt{2}}\left( \phi_{200} \pm\phi_{210} \right)$\egroup$ with energies of $\bgroup\color{black}$E_2$\egroup$ , $\bgroup\color{black}$E_2$\egroup$ , and $\bgroup\color{black}$E_2\mp 3e{\cal E}a_0$\egroup$ .

Jim Branson 2013-04-22