Next: Derivations and Computations Up: Examples Previous: Hydrogen Atom Ground State Contents
The Stark effect for the n=2 states of hydrogen requires the use of
degenerate state perturbation theory since there are four states
with (nearly) the same energies.
For our first calculation, we will ignore the hydrogen fine structure
and assume that the four states are exactly degenerate, each with unperturbed
energy of
![]() .
That is
.
That is
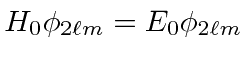 .
The degenerate states
.
The degenerate states
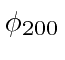 ,
,
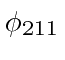 ,
,
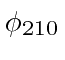 , and
, and
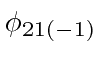 .
.
The perturbation due to an electric field in the z direction is
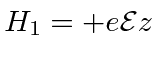 .
So our first order degenerate state perturbation theory equation is
.
So our first order degenerate state perturbation theory equation is
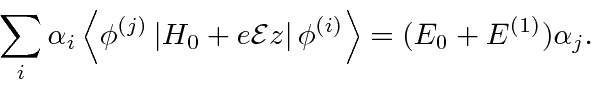
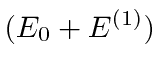 , distinguished by the index
, distinguished by the index
Because of the exact degeneracy
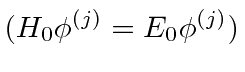 ,
,
![]() and
and
![]() can be eliminated from the equation.
can be eliminated from the equation.
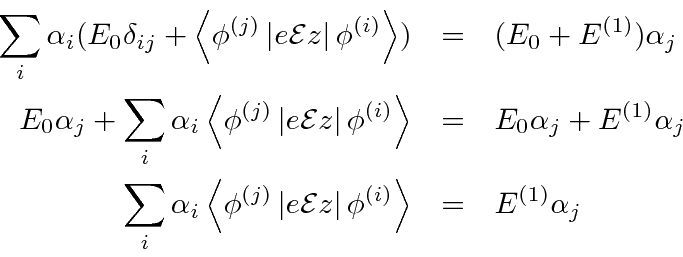
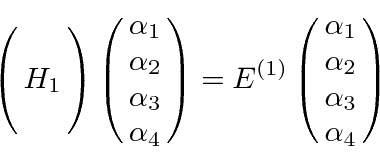
![\bgroup\color{black}$[L_z,z]=0$\egroup](img3013.png) , that all the matrix elements between states of unequal
, that all the matrix elements between states of unequal
![\begin{displaymath}\bgroup\color{black}\left< Y_{lm}\left\vert[L_z,z]\right\vert...
...') \left<Y_{lm}\left\vert z \right\vert Y_{l'm'}\right> \egroup\end{displaymath}](img3014.png)
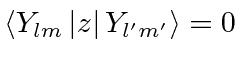 unless
unless
Lets define the one remaining nonzero (real) matrix element to be
![]() .
.
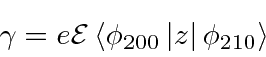
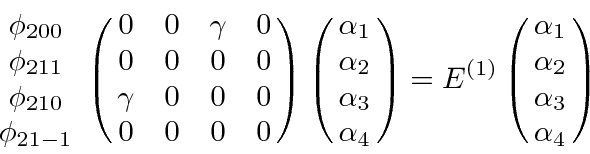
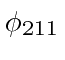 ,
,
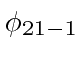 , and
, and
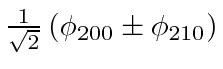 with eigenvalues (of
with eigenvalues (of
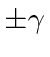 .
.
What remains is to compute
![]() .
Recall
.
Recall
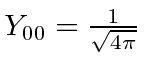 and
and
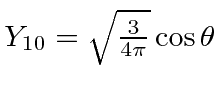 .
.
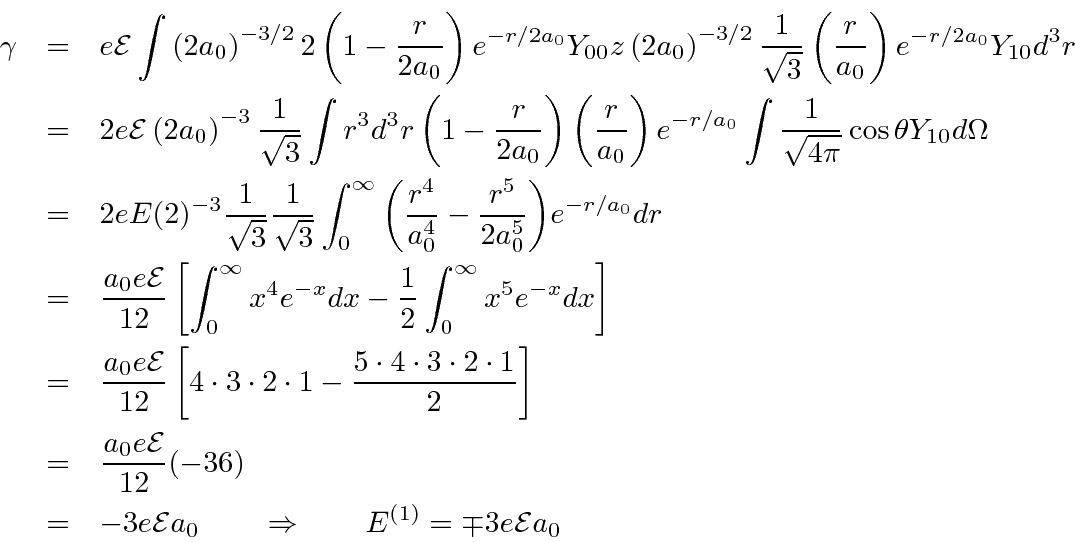
If the states are not exactly degenerate, we have to leave in the diagonal terms of
![]() .
Assume that the energies of the two (mixed) states are
.
Assume that the energies of the two (mixed) states are
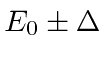 ,
where
,
where
![]() comes from some other perturbation, like the hydrogen fine structure.
(The
comes from some other perturbation, like the hydrogen fine structure.
(The
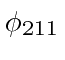 and
and
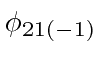 are still not mixed by the electric field.)
are still not mixed by the electric field.)
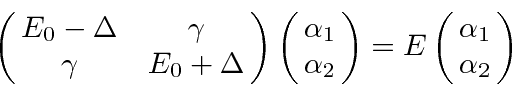
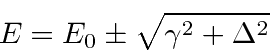
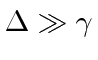 , and
, and
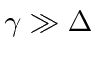 .
It is also correct when the two corrections are of the same order.
.
It is also correct when the two corrections are of the same order.
Jim Branson 2013-04-22