Next: Homework Problems Up: Derivations and Computations Previous: Derivation of 1st and Contents
To deal with the problem of degenerate states, we will allow an arbitrary linear combination
of those states at zeroth order.
In the following equation, the sum over
![]() is the sum over all the states degenerate with
is the sum over all the states degenerate with
![]() and the sum over k runs over all the other states.
and the sum over k runs over all the other states.
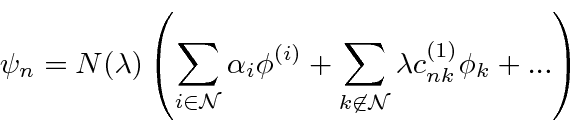
The full Schrödinger equation is.
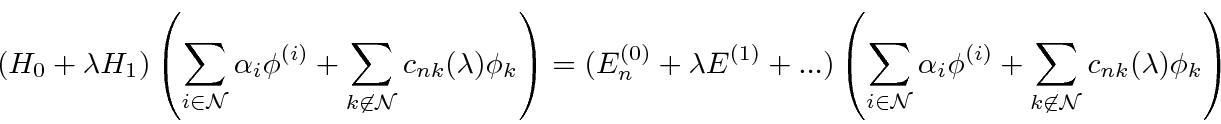
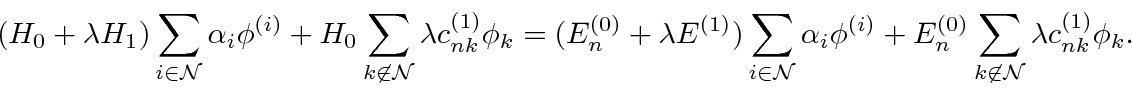
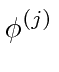 , we get
, we get
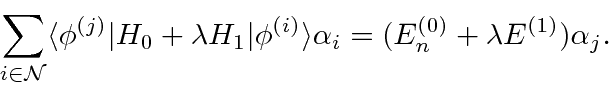
By putting both terms together, our calculation gives us the full energy to first order, not just the
correction.
It is useful both for degenerate states and for nearly degenerate states.
The result may be simplified to
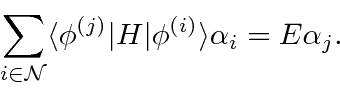
Jim Branson 2013-04-22