Next: Sample Test Problems Up: Time Independent Perturbation Theory Previous: Derivation of 1st Order Contents
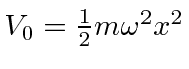 . Small electric fields in the
. Small electric fields in the 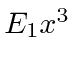 is applied.
is applied.
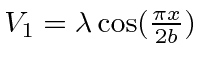 is applied. Calculate the energies of the first and second
excited states in this new potential.
is applied. Calculate the energies of the first and second
excited states in this new potential.
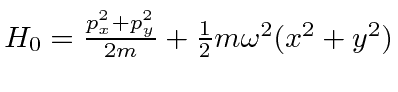 .
Calculate the energy shifts of the ground state and the
degenerate first excited states, to first order,
if the additional potential
.
Calculate the energy shifts of the ground state and the
degenerate first excited states, to first order,
if the additional potential 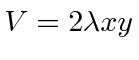 is applied.
Now solve the problem exactly.
Compare the exact result for the ground state to that
from second order perturbation theory.
is applied.
Now solve the problem exactly.
Compare the exact result for the ground state to that
from second order perturbation theory.
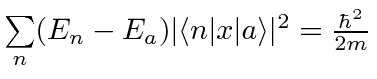 by starting from the expectation value of the commutator
by starting from the expectation value of the commutator
![$[p,x]$](img3060.png) in the state
in the state 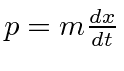 and write
and write ![$[H,x]$](img3063.png) to get the result.
to get the result.
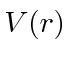 is
is
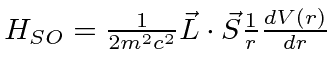 ,
what is the effect of that coupling on the spectrum of a three
dimensional harmonic oscillator?
Compute the relativistic correction for the ground state
of the three dimensional harmonic oscillator.
,
what is the effect of that coupling on the spectrum of a three
dimensional harmonic oscillator?
Compute the relativistic correction for the ground state
of the three dimensional harmonic oscillator.
Jim Branson 2013-04-22