- Assume an electron is bound to a heavy positive
particle with a harmonic potential
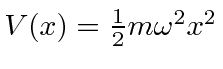 .
Calculate the energy shifts to all the energy eigenstates in an
electric field
.
Calculate the energy shifts to all the energy eigenstates in an
electric field 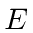 (in the
(in the 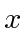 direction).
direction).
- Find the energies of the
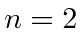 hydrogen states in a strong
uniform electric field in the z-direction. (Note, since spin plays no
role here there are just 4 degenerate states. Ignore the fine structure
corrections to the energy since the E-field is strong.
Remember to use the fact that
hydrogen states in a strong
uniform electric field in the z-direction. (Note, since spin plays no
role here there are just 4 degenerate states. Ignore the fine structure
corrections to the energy since the E-field is strong.
Remember to use the fact that ![$[L_z,z]=0$](img3068.png) .
If you are pressed
for time, don't bother to evaluate the radial integrals.)
.
If you are pressed
for time, don't bother to evaluate the radial integrals.)
- An electron is in a three dimensional harmonic oscillator potential
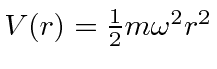 .
A small electric field, of strength
.
A small electric field, of strength 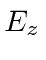 , is applied in the
, is applied in the 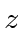 direction.
Calculate the lowest order nonzero correction to the ground state energy.
direction.
Calculate the lowest order nonzero correction to the ground state energy.
- Hydrogen atoms in the
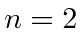 state are put in a strong Electric field.
Assume that the 2s and 2p states of Hydrogen are degenerate and spin is not important.
Under these assumptions, there are 4 states: the 2s and three 2p states.
Calculate the shifts in energy due to the E-field and give the states that have
those energies.
Please work out the problem in principle before attempting any integrals.
state are put in a strong Electric field.
Assume that the 2s and 2p states of Hydrogen are degenerate and spin is not important.
Under these assumptions, there are 4 states: the 2s and three 2p states.
Calculate the shifts in energy due to the E-field and give the states that have
those energies.
Please work out the problem in principle before attempting any integrals.
Jim Branson
2013-04-22
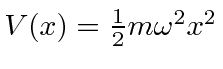 .
Calculate the energy shifts to all the energy eigenstates in an
electric field
.
Calculate the energy shifts to all the energy eigenstates in an
electric field ![$[L_z,z]=0$](img3068.png) .
If you are pressed
for time, don't bother to evaluate the radial integrals.)
.
If you are pressed
for time, don't bother to evaluate the radial integrals.)
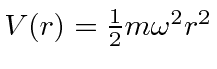 .
A small electric field, of strength
.
A small electric field, of strength