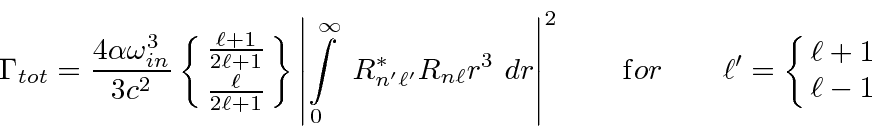Review of Radiation of Photons

In the previous section, we derived the same formulas for matrix elements that we had earlier used to study decays of Hydrogen atom states with no applied EM field, that is zero photons in the initial state.

$$\begin{eqnarray*} \Gamma_{i\rightarrow n}&=&{(2\pi)^2e^2\over m^2\omega V} \vert... ...vec{p}\vert\phi_i\rangle\vert^2\:\delta(E_n-E_i+\hbar\omega) \\ \end{eqnarray*}$$

With the inclusion of the phase space integral over final states this became

$$\bgroup\color{black} \Gamma_{tot}={e^2(E_i-E_n)\over 2\pi\hba... ...lon}^{(\lambda)}\cdot\vec{p_e}\vert\phi_i\rangle\vert^2 \egroup$$

The quantity $\vec{k}\cdot\vec{r}$ is typically small for atomic transitions

$$\begin{eqnarray*} E_\gamma=pc=\hbar kc\approx {1\over 2}\alpha^2mc^2 \\ r\appro... ...}{\alpha^2mc\over\hbar}{\hbar\over\alpha mc}={\alpha\over 2} \\ \end{eqnarray*}$$

Note that we have take the full binding energy as the energy difference between states so almost all transitions will have $kr$ smaller than this estimate. This makes $\vec{k}\cdot\vec{r}$ an excellent parameter in which to expand decay rate formulas.

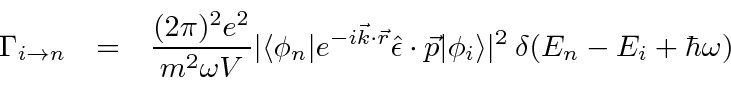
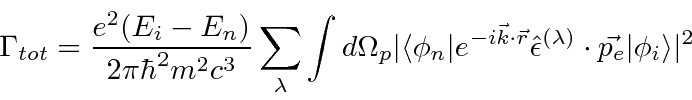
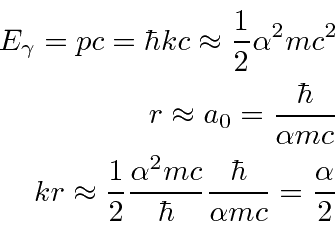
The approximation that $e^{-i\vec{k}\cdot\vec{r}}\approx 1$ is a very good one and is called the electric dipole or E1 approximation. We previously derived the E1 selection rules.

$$\begin{eqnarray*} \Delta\ell&=&\pm 1. \\ \Delta m&=&0,\pm 1. \\ \Delta s&=&0. \\ \end{eqnarray*}$$

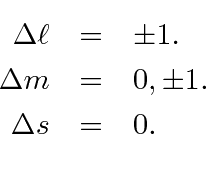
The general E1 decay result depends on photon direction and polarization. If information about angular distributions or polarization is needed, it can be pried out of this formula.

$$\begin{eqnarray*} \Gamma_{tot}&=&{e^2(E_i-E_n)\over 2\pi\hbar^2 m^2c^3}\sum\limi... ...ilon_y\over\sqrt{2}}Y_{1-1}\right)Y_{\ell_im_i}\right\vert^2 \\ \end{eqnarray*}$$

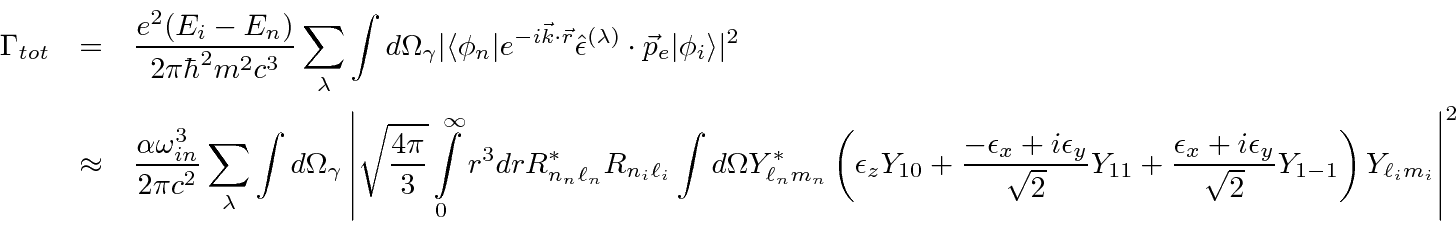
Summing over polarization and integrating over photon direction, we get a simpler formula that is quite useful to compute the decay rate from one initial atomic state to one final atomic state.

$$\bgroup\color{black} \Gamma_{tot}={4\alpha\omega_{in}^3\over 3c^2}\vert\vec{r}_{ni}\vert^2 \egroup$$

Here $\vec{r}_{ni}$ is the matrix element of the coordinate vector between final and initial states.

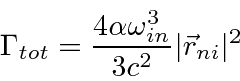
For single electron atoms, we can sum over the final states with different $m$ and get a formula only requires us to do a radial integral.

$$\bgroup\color{black} \Gamma_{tot}={4\alpha\omega_{in}^3\over ... ...or}\qquad \ell'=\left\{\matrix{\ell+1\cr \ell-1}\right. \egroup$$

The decay rate does not depend on the $m$ of the initial state.