Emission and Absorption of Photons by Atoms

The interaction of an electron with the quantized field is already in the standard Hamiltonian.

$$\begin{eqnarray*} H&=&{1\over 2m}\left(\vec{p}+{e\over c}\vec{A}\right)^2+V(r) \... ...r mc}\vec{A}\cdot\vec{p}+{e^2\over 2mc^2}\vec{A}\cdot\vec{A} \\ \end{eqnarray*}$$

For completeness we should add the interaction with the spin of the electron $H=-\vec{\mu}\cdot\vec{B}$.

$$H_{int}=-{e\over mc}\vec{A}\cdot\vec{p}+{e^2\... ...cdot\vec{A} -{e\hbar\over 2mc}\vec{\sigma}\cdot\vec{\nabla}\times\vec{A}$$

For an atom with many electrons, we must sum over all the electrons. The field is evaluated at the coordinate $x$ which should be that of the electron.

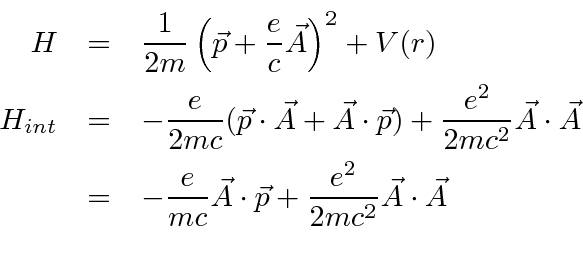
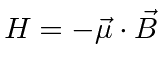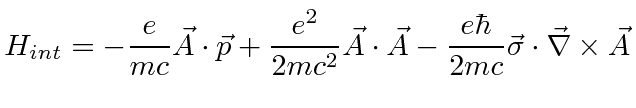This interaction Hamiltonian contains operators to create and annihilate photons with transitions between atomic states. From our previous study of time dependent perturbation theory, we know that transitions between initial and final states are proportional to the matrix element of the perturbing Hamiltonian between the states, 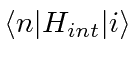$\langle n\vert H_{int}\vert i\rangle$. The initial state $\vert i\rangle$ should include a direct product of the atomic state and the photon state. Lets concentrate on one type of photon for now. We then could write

$$\bgroup\color{black} \vert i\rangle=\vert\psi_i;n_{\vec{k},\alpha}\rangle \egroup$$

with a similar expression for the final state.

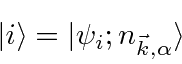
We will first consider the absorption of one photon from the field. Assume there are 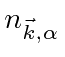$n_{\vec{k},\alpha}$ photons of this type in the initial state and that one photon is absorbed. We therefore will need a term in the interaction Hamiltonian that contains on annihilation operator (only). This will just come from the linear term in A.

$$\begin{eqnarray*} \langle n\vert H_{int}\vert i\rangle&=&\langle\psi_n;n_{\vec{k... ...}^{(\alpha)}\cdot\vec{p} \vert\psi_i\rangle e^{-i\omega t} \\ \end{eqnarray*}$$

Similarly, for the emission of a photon the matrix element is.

$$\begin{eqnarray*} \langle n\vert H_{int}\vert i\rangle&=&\langle\psi_n;n_{\vec{k... ...lon}^{(\alpha)}\cdot\vec{p} \vert\psi_i\rangle e^{i\omega t} \\ \end{eqnarray*}$$

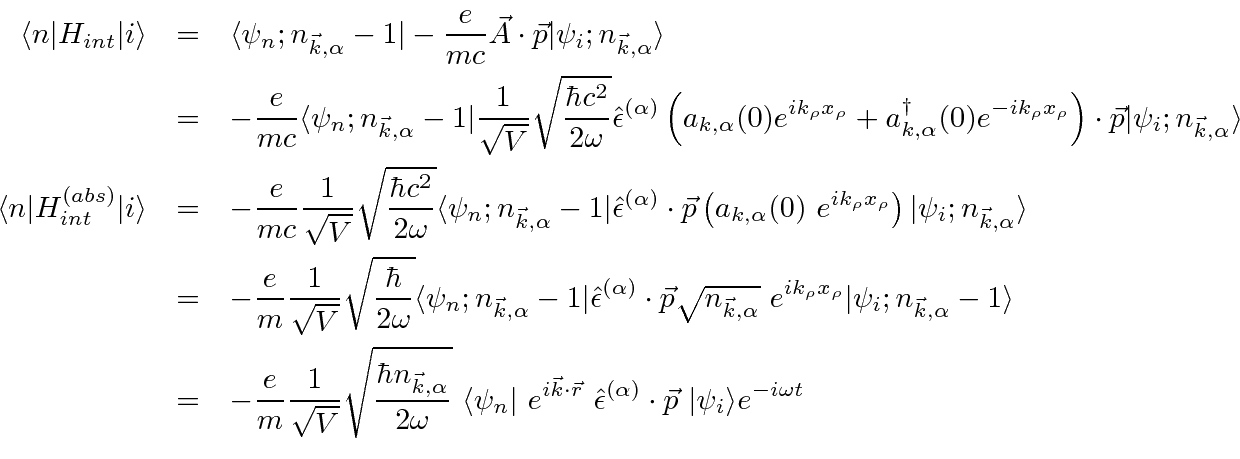
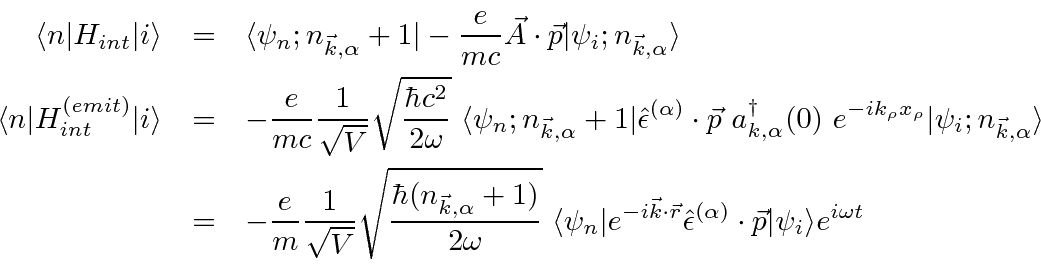
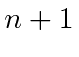These give the same result as our earlier guess to put an $n+1$ in the emission operator.