Next: Emission and Absorption of Up: Quantum Theory of Radiation Previous: The Time Development of Contents
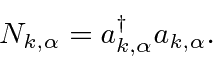
Of course the average value of the Electric or Magnetic field vector is zero by symmetry.
To get an idea about the size of field fluctuations, we should look at the mean square value of the field,
for example in the vacuum state.
We compute
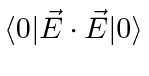 .
.
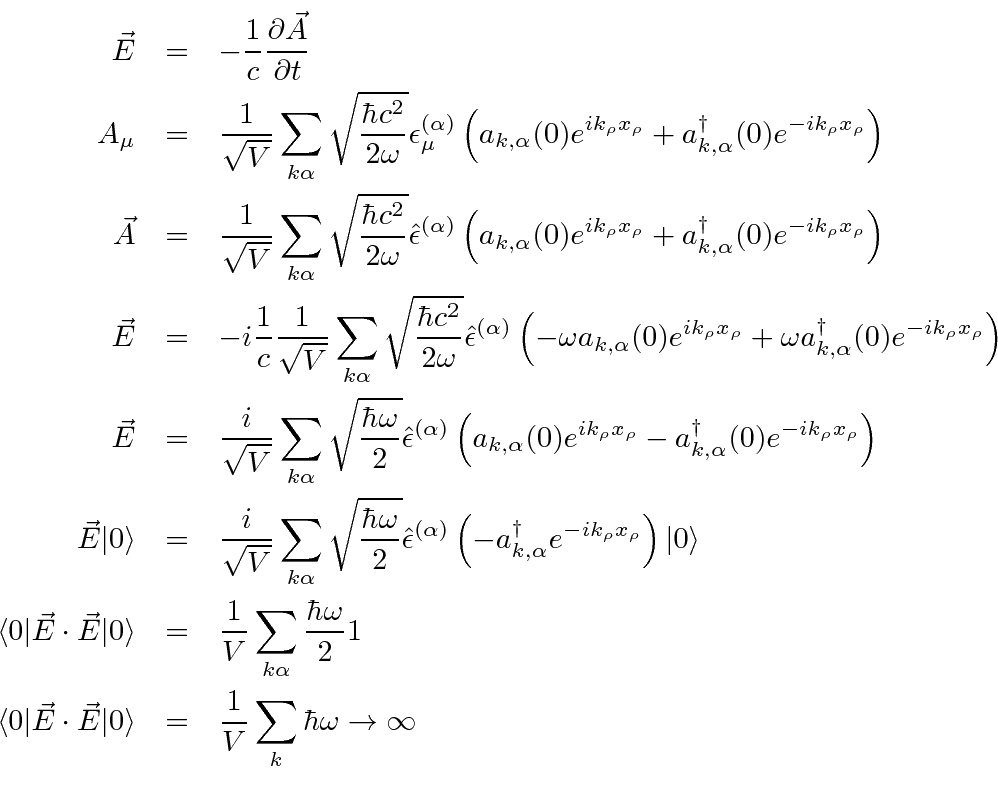
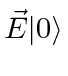 and that the orthogonality of the states collapses the result down to a single sum.)
and that the orthogonality of the states collapses the result down to a single sum.)
The calculation is illustrative even though the answer is infinite.
Basically, a term proportional to
![]() first creates one photon then absorbs it giving a nonzero contribution
for every oscillator mode.
The terms sum to infinity but really its the infinitesimally short wavelengths that cause this.
Again, some cut off in the maximum energy would make sense.
first creates one photon then absorbs it giving a nonzero contribution
for every oscillator mode.
The terms sum to infinity but really its the infinitesimally short wavelengths that cause this.
Again, some cut off in the maximum energy would make sense.
The effect of these field fluctuations on particles is mitigated by quantum mechanics.
In reality, any quantum particle will be spread out over a finite volume and its the average field over
the volume that might cause the particle to experience a force.
So we could average the Electric field over a volume, then take the mean square of the average.
If we average over a cubic volume
![]() , then we find that
, then we find that
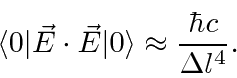
Even the E and B fields do not commute.
It can be shown that
![\begin{displaymath}\bgroup\color{black} [E_x(x),B_y(x')]=ic\hbar \delta(ds=\sqrt{(x-x')_\rho(x-x')_\rho}) \egroup\end{displaymath}](img3977.png)
To make a narrow beam of light, one must adjust the phases of various components of the beam carefully.
Another version of the uncertainty relation is that
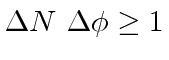 ,
where
,
where
![]() is the phase of a Fourier component and
is the phase of a Fourier component and
![]() is the number of photons.
is the number of photons.
Of course the Electromagnetic waves of classical physics usually have very large numbers of photons and the quantum effects are not apparent. A good condition to identify the boundary between classical and quantum behavior is that for the classical E&M to be correct the number of photons per cubic wavelength should be much greater than 1.
Jim Branson 2013-04-22