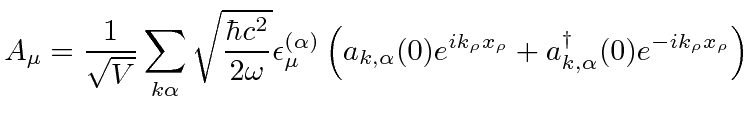The creation and annihilation operators are related to the
time dependent coefficients in our Fourier expansion of the radiation field.
This means that the creation, annihilation, and other operators are time dependent operators
as we have studied the
Heisenberg representation.
In particular, we derived the canonical equation for the time dependence of an operator.
So the operators have the same time dependence as did the coefficients in the Fourier expansion.
We can now write the quantized radiation field in terms of the operators at
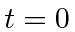 .
.
Again, the 4-vector
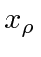 is a parameter of this field, not the location of a photon.
The field operator is Hermitian and the field itself is real.
is a parameter of this field, not the location of a photon.
The field operator is Hermitian and the field itself is real.
Jim Branson
2013-04-22
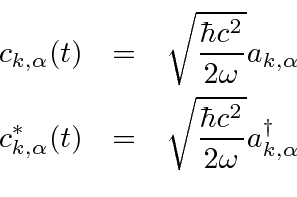
![\begin{eqnarray*}
{d\over dt}B(t)&=&{i\over\hbar}[H,B(t)] \\
\dot{a}_{k,\alpha}...
...}[H,a_{k,\alpha}^\dagger(t)]=i\omega a_{k,\alpha}^\dagger(t) \\
\end{eqnarray*}](img3966.png)
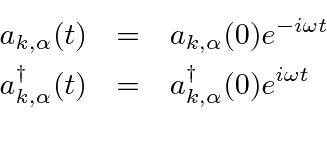
![]() .
.