Next: The Time Development of Up: Quantum Theory of Radiation Previous: Fermion Operators Contents
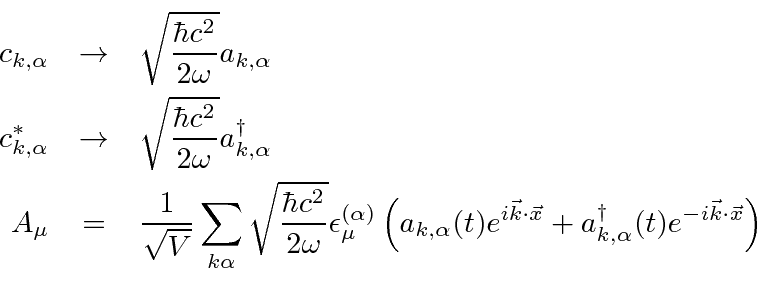
The Hamiltonian operator can also be written in terms of the creation and annihilation operators.
![\begin{eqnarray*}
H&=&\sum\limits_{k,\alpha}\left({\omega\over c}\right)^2\left[...
..._{k,\alpha}^\dagger+a_{k,\alpha}^\dagger a_{k,\alpha}\right] \\
\end{eqnarray*}](img3950.png)
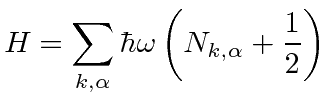 |
For our purposes, we may remove the (infinite) constant energy due to the ground state energy of all the oscillators.
It is simply the energy of the vacuum which we may define as zero.
Note that the field fluctuations that cause this energy density, also cause the spontaneous decay of excited states of atoms.
One thing that must be done is to cut off the sum at some maximum value of
![]() .
We do not expect electricity and magnetism to be completely valid up to infinite energy.
Certainly by the gravitational or grand unified energy scale there must be important corrections to our formulas.
The energy density of the vacuum is hard to define but plays an important role in cosmology.
At this time, physicists have difficulty explaining how small the energy density in the vacuum is.
Until recent experiments showed otherwise, most physicists thought it was actually zero due to some unknown symmetry.
In any case we are not ready to consider this problem.
.
We do not expect electricity and magnetism to be completely valid up to infinite energy.
Certainly by the gravitational or grand unified energy scale there must be important corrections to our formulas.
The energy density of the vacuum is hard to define but plays an important role in cosmology.
At this time, physicists have difficulty explaining how small the energy density in the vacuum is.
Until recent experiments showed otherwise, most physicists thought it was actually zero due to some unknown symmetry.
In any case we are not ready to consider this problem.
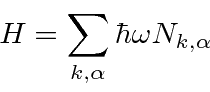
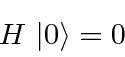
The total momentum in the (transverse) radiation field can also be computed
(from the classical formula for the Poynting vector).
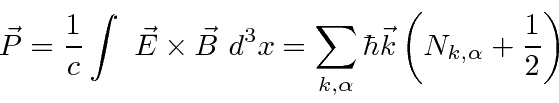
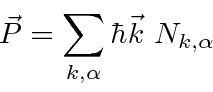
We can compute the energy and momentum of a single photon state by operating on that state with the Hamiltonian
and with the total momentum operator.
The state for a single photon with a given momentum and polarization can be written as
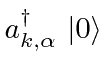 .
.
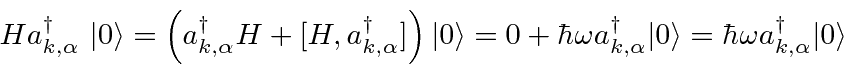
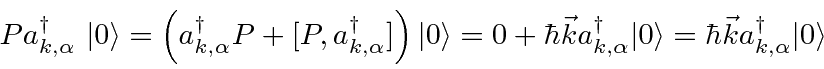
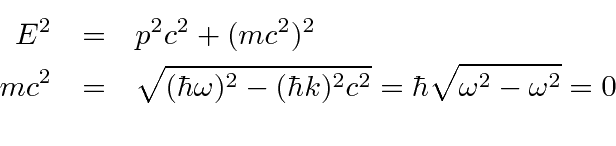
The vector potential has been given two transverse polarizations as expected from classical Electricity and Magnetism. The result is two possible transverse polarization vectors in our quantized field. The photon states are also labeled by one of two polarizations, that we have so far assumed were linear polarizations. The polarization vector, and therefore the vector potential, transform like a Lorentz vector. We know that the matrix element of vector operators is associated with an angular momentum of one. When a photon is emitted, selection rules indicate it is carrying away an angular momentum of one, so we deduce that the photon has spin one. We need not add anything to our theory though; the vector properties of the field are already included in our assumptions about polarization.
Of course we could equally well use circular polarizations which are related to the linear set we have been using by
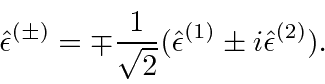
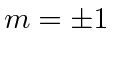 component of the photon's spin.
These are the transverse mode of the photon,
component of the photon's spin.
These are the transverse mode of the photon,
By assuming the canonical coordinates and momenta in the Hamiltonian have commutators like those of the position and momentum of a particle, led to an understanding that radiation is made up of spin-1 particles with mass zero. All fields correspond to a particle of definite mass and spin. We now have a pretty good idea how to quantize the field for any particle.
Jim Branson 2013-04-22