Next: Exponential Decay Up: Radiation in Atoms Previous: Angular Distributions Contents
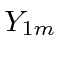 .
We found that the
.
We found that the
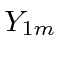 could change the orbital angular momentum (from initial to final state) by zero or one unit.
This will be true for any vector operator.
could change the orbital angular momentum (from initial to final state) by zero or one unit.
This will be true for any vector operator.
In fact, because the vector operator is very much like adding an additional
![]() to the initial state angular momentum,
Wigner and Eckart proved that all matrix elements of vector operators can be written as a
reduced matrix element which does not depend on any of the
to the initial state angular momentum,
Wigner and Eckart proved that all matrix elements of vector operators can be written as a
reduced matrix element which does not depend on any of the
![]() ,
and Clebsch-Gordan coefficients.
The basic reason for this is that all vectors transform the same way under rotations,
so all have the same angular properties, being written in terms of the
,
and Clebsch-Gordan coefficients.
The basic reason for this is that all vectors transform the same way under rotations,
so all have the same angular properties, being written in terms of the
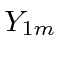 .
.
Note that it makes sense to write a vector
![]() in terms of the spherical harmonics using
in terms of the spherical harmonics using
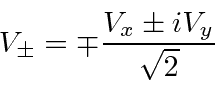
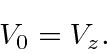
Lets consider our vector
![]() where the integer
where the integer
![]() runs from -1 to +1.
The Wigner-Eckart theorem says
runs from -1 to +1.
The Wigner-Eckart theorem says
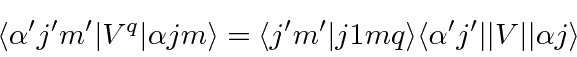
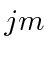 represent the usual angular momentum quantum numbers of the states.
represent the usual angular momentum quantum numbers of the states.
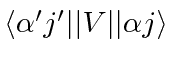 is a reduced matrix element.
Its the same for all values of
is a reduced matrix element.
Its the same for all values of
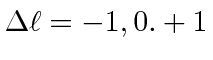 .
.
The theorem can be generalized for spherical tensors of higher (or even lower) rank than a vector.
Jim Branson 2013-04-22