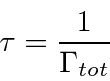We have computed transition rates using our theory of radiation.
In doing this, we have assumed that our calculations need only be valid near
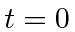 .
More specifically, we have assumed that we start out in some initial state
.
More specifically, we have assumed that we start out in some initial state
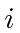 and that
the amplitude to be in that initial state is one.
The probability to be in the initial state will become depleted for times on the order of the lifetime
of the state.
We can account for this in terms of the probability to remain in the initial state.
and that
the amplitude to be in that initial state is one.
The probability to be in the initial state will become depleted for times on the order of the lifetime
of the state.
We can account for this in terms of the probability to remain in the initial state.
Assume we have computed the total transition rate.
This transition rate is the probability per unit time to make a transition away from the initial state
evaluated at
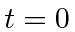 .
Writing this as an equation we have.
.
Writing this as an equation we have.
For larger times we can assume that the probability to make a transition away from the initial state
is proportional to the probability to be in the initial state.
The solution to this simple first order differential equation is
If you are having any trouble buying this calculation,
think of a large ensemble of hydrogen atoms prepared to be in the 2p state at
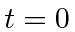 .
Clearly the number of atoms remaining in the 2p state will obey the equation
.
Clearly the number of atoms remaining in the 2p state will obey the equation
and we will have our exponential time distribution.
We may define the lifetime of a state to the the time after which only
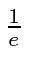 of the decaying state remains.
of the decaying state remains.
Jim Branson
2013-04-22
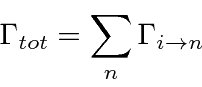
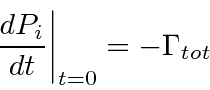
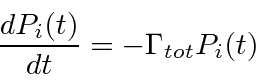
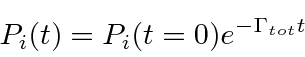
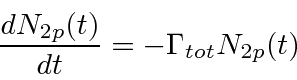
![]() of the decaying state remains.
of the decaying state remains.