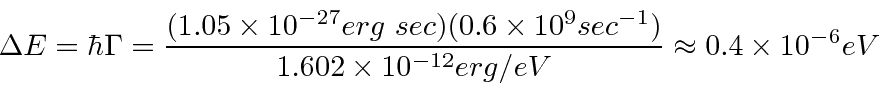Now we have computed the lifetime of a state.
For some atomic, nuclear, or particle states, this lifetime can be very short.
We know that energy conservation can be violated for short times according to the uncertainty principle
This means that a unstable state can have an energy width on the order of
We may be more quantitative.
If the probability to be in the initial state is proportional to
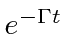 , then we have
, then we have
We may take the Fourier transform of this time function to the the amplitude as a function of frequency.
We may square this to get the probability or intensity as a function of
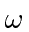 (and hence
(and hence
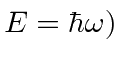 .
.
This gives the energy distribution of an unstable state.
It is called the Breit-Wigner line shape.
It can be characterized by its Full Width at Half Maximum (FWHM) of
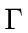 .
.
The Breit-Wigner will be the observed line shape as long as the density of final states is nearly
constant over the width of the line.
As
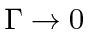 this line shape approaches a delta function,
this line shape approaches a delta function,
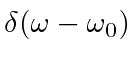 .
.
For the 2p to 1s transition in hydrogen, we've calculated a decay rate of
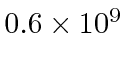 per second.
We can compute the FWHM of the width of the photon line.
per second.
We can compute the FWHM of the width of the photon line.
Since the energy of the photon is about 10 eV, the width is about
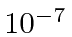 of the photon energy.
Its narrow but not enough for example make an atomic clock.
Weaker transitions, like those from E2 or M1 will be relatively narrower, allowing use in precision systems.
of the photon energy.
Its narrow but not enough for example make an atomic clock.
Weaker transitions, like those from E2 or M1 will be relatively narrower, allowing use in precision systems.
Subsections
Jim Branson
2013-04-22
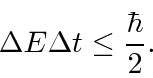
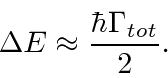
![]() , then we have
, then we have
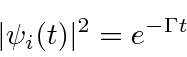
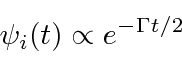
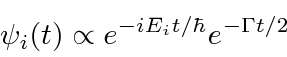
![\begin{eqnarray*}
\phi_i(\omega) &\propto& \int\limits_0^\infty \psi_i(t) e^{i\o...
...ht]_0^\infty \\
&=& {i\over (\omega-\omega_0+i{\Gamma\over 2})}
\end{eqnarray*}](img3664.png)
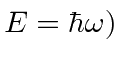 .
.
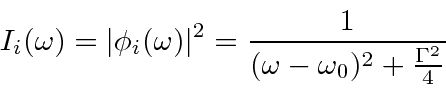
![]() this line shape approaches a delta function,
this line shape approaches a delta function,
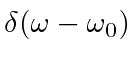 .
.
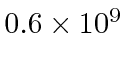 per second.
We can compute the FWHM of the width of the photon line.
per second.
We can compute the FWHM of the width of the photon line.