Next: Vector Operators and the Up: Radiation in Atoms Previous: General Unpolarized Initial State Contents
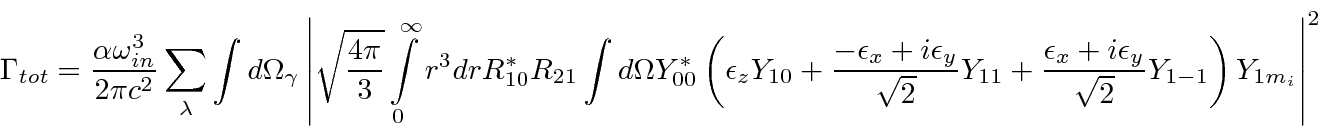
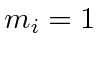 .
We then look at our result for the angular integration in the matrix element
.
We then look at our result for the angular integration in the matrix element
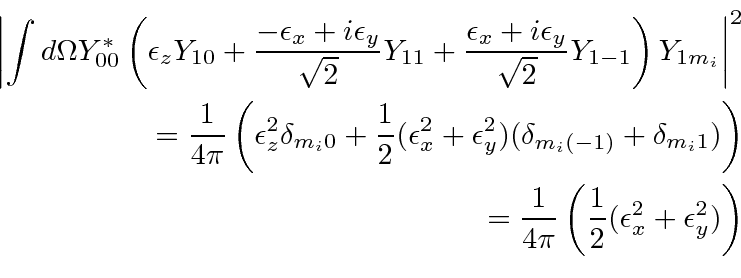
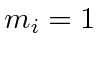 eliminating two terms.
eliminating two terms.
Lets study the rate as a function of the angle of the photon from the z axis,
![]() .
The rate will be independent of the azimuthal angle.
We see that the rate is proportional to
.
The rate will be independent of the azimuthal angle.
We see that the rate is proportional to
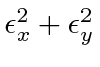 .
We still must sum over the two independent transverse polarizations.
For clarity, assume that
.
We still must sum over the two independent transverse polarizations.
For clarity, assume that
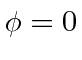 and the photon is therefore emitted in the x-z plane.
One transverse polarization can be in the y direction.
The other is in the x-z plane perpendicular to the direction of the photon.
The x component is proportional to
and the photon is therefore emitted in the x-z plane.
One transverse polarization can be in the y direction.
The other is in the x-z plane perpendicular to the direction of the photon.
The x component is proportional to
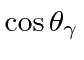 .
So the rate is proportional to
.
So the rate is proportional to
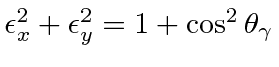 .
.
If we assume that
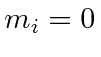 then only the
then only the
![]() term remains
and the rate is proportional to
term remains
and the rate is proportional to
![]() .
The angular distribution then goes like
.
The angular distribution then goes like
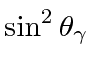 .
.
Jim Branson 2013-04-22