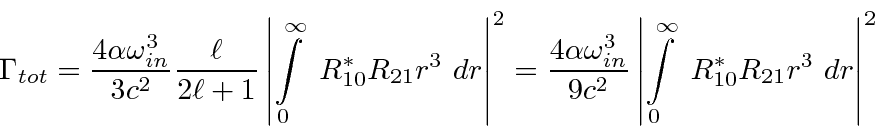General Unpolarized Initial State
If we are just interested in the total decay rate, we can go further.
The decay rate should not depend on the polarization of the initial state, based on the rotational symmetry of our theory.
Usually we only want the total decay rate to some final state so we sum over polarizations of the photon,
integrate over photon directions, and (eventually)
sum over the different
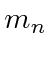 of the final state atoms.
We begin with a simple version of the total decay rate formula in the E1 approximation.
of the final state atoms.
We begin with a simple version of the total decay rate formula in the E1 approximation.
Where
 is the angle between the matrix element of the position vector
is the angle between the matrix element of the position vector
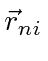 and the polarization vector
and the polarization vector
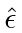 .
It is far easier to understand the sum over polarizations in terms of familiar vectors in 3-space than
by using sums of Clebsch-Gordan coefficients.
.
It is far easier to understand the sum over polarizations in terms of familiar vectors in 3-space than
by using sums of Clebsch-Gordan coefficients.
Lets pick two transverse polarization vectors (to sum over) that form a right handed system with the
direction of photon propagation.
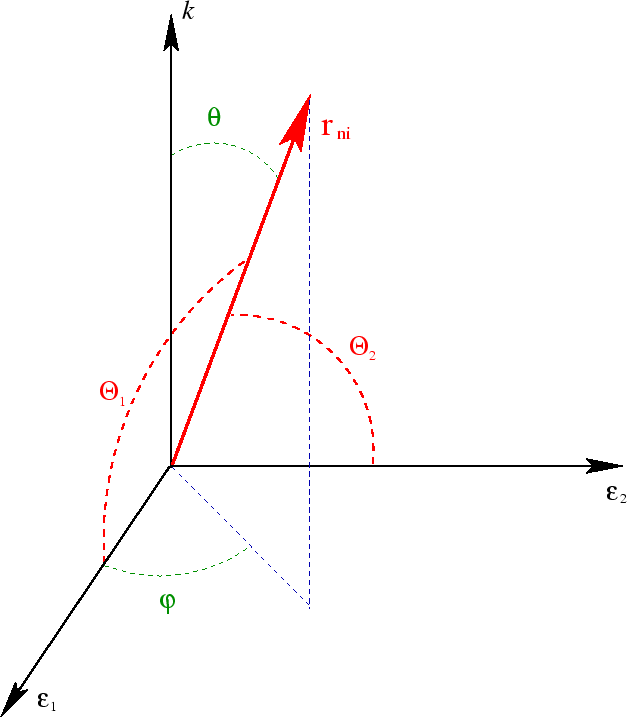
The figure below shows the angles, basically picking the photon direction as the polar axis,
and the
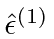 direction as what is usually called the x-axis.
The projection of the vector
direction as what is usually called the x-axis.
The projection of the vector
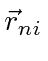 into the transverse plan gives a factor of
into the transverse plan gives a factor of
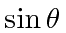 .
It is then easy to see that
.
It is then easy to see that
The sum of
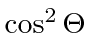 over the two polarizations then just gives
over the two polarizations then just gives
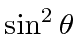 .
Therefore the decay rate becomes
.
Therefore the decay rate becomes
This is now a very nice and simple result for the total decay rate of a state, summed over photon polarizations
and integrated over photon direction.
We still need to sum over the final atomic states as necessary.
For the case of a transition in a single electron atom
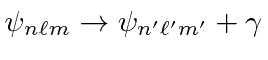 ,
summed over
,
summed over
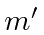 ,
the properties of the Clebsch-Gordan coefficients can be used to show
(See Merzbacher, second edition, page 467).
,
the properties of the Clebsch-Gordan coefficients can be used to show
(See Merzbacher, second edition, page 467).
The result is independent of
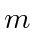 as we would expect from rotational symmetry.
as we would expect from rotational symmetry.
As a simple check, lets recompute the 2p to 1s decay rate for hydrogen.
We must choose the
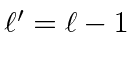 case and
case and
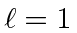 .
.
This is the same result we got in the explicit calculation.
Jim Branson
2013-04-22
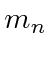 of the final state atoms.
We begin with a simple version of the total decay rate formula in the E1 approximation.
of the final state atoms.
We begin with a simple version of the total decay rate formula in the E1 approximation.
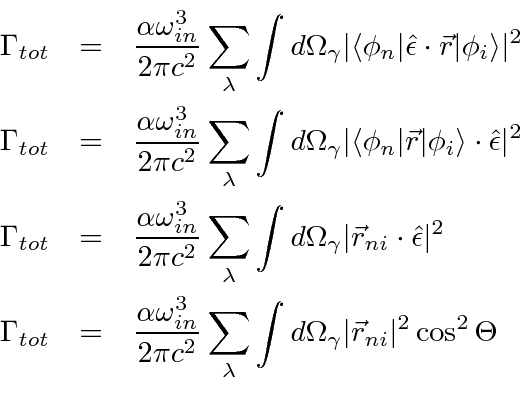
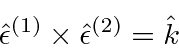
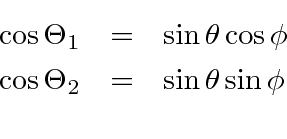
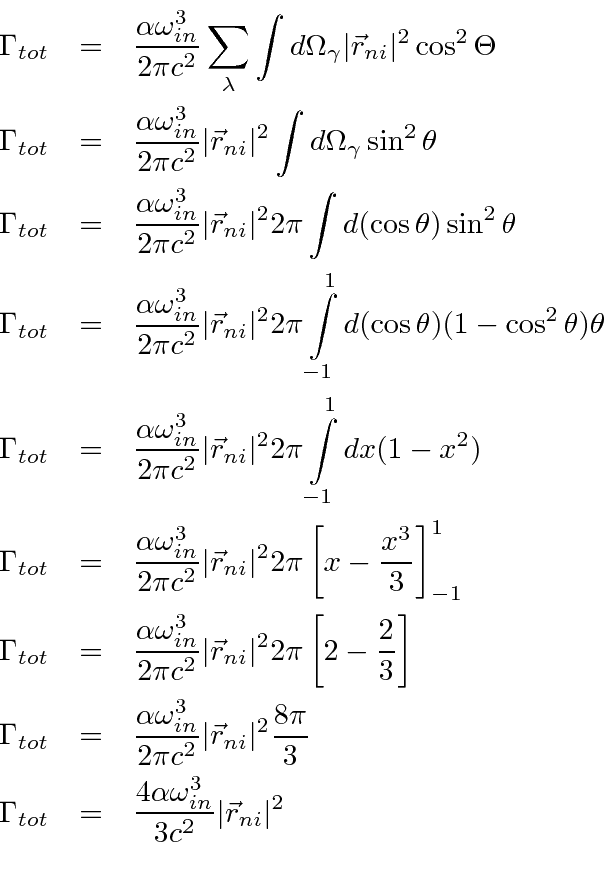
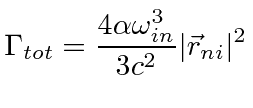
 ,
summed over
,
summed over
![]() ,
the properties of the Clebsch-Gordan coefficients can be used to show
(See Merzbacher, second edition, page 467).
,
the properties of the Clebsch-Gordan coefficients can be used to show
(See Merzbacher, second edition, page 467).
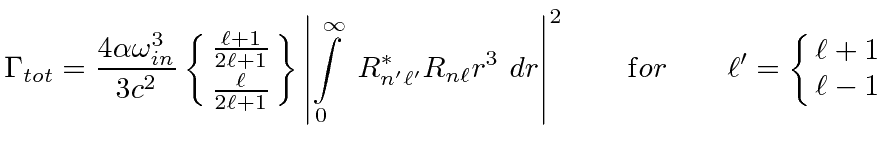
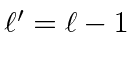 case and
case and
![]() .
.