Next: General Unpolarized Initial State Up: Radiation in Atoms Previous: Electric Dipole Approximation and Contents
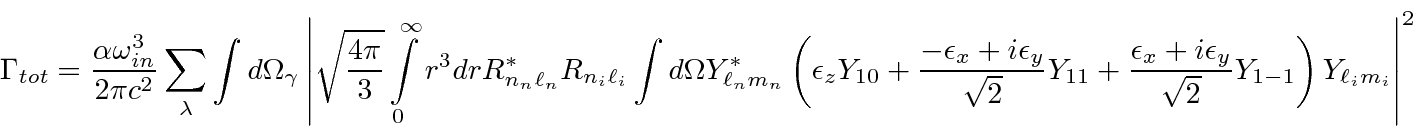
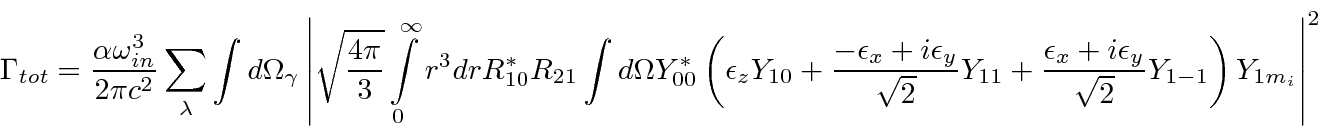
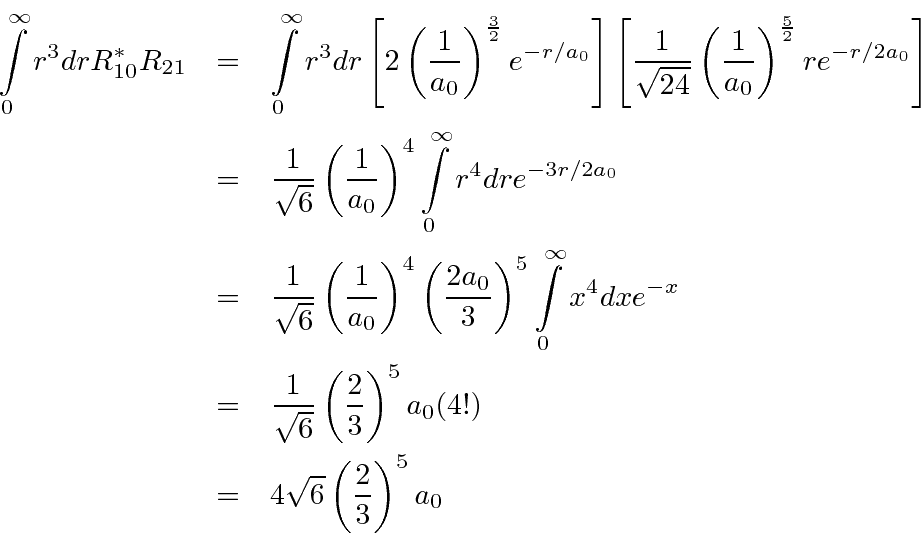
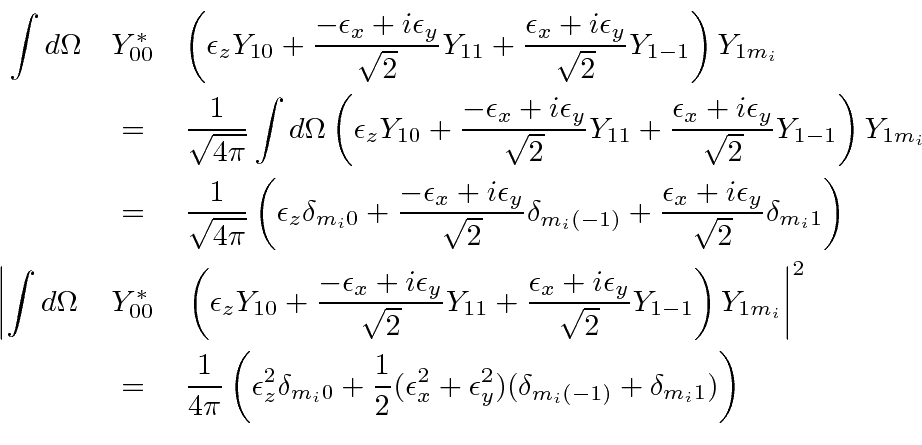
Lets assume the initial state is unpolarized, so we will sum over
![]() and divide by 3,
the number of different
and divide by 3,
the number of different
![]() allowed.
allowed.
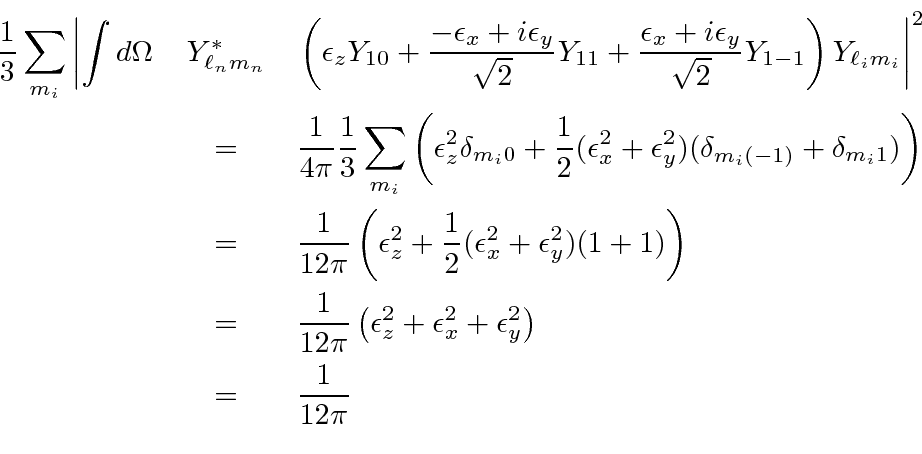
Our result is independent of photon polarization since we assumed the initial state was unpolarized, but,
we must still sum over photon polarization.
Lets assume that we are not interested in measuring the photon's polarization.
The polarization vector is constrained to be perpendicular to the photons direction
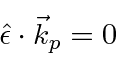
The integral over photon direction clearly just gives a factor of
![]() since there is no
direction dependence left in the integrand (due to our assumption of an unpolarized initial state).
since there is no
direction dependence left in the integrand (due to our assumption of an unpolarized initial state).
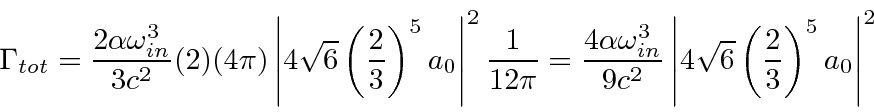
Jim Branson 2013-04-22